Ejercicio Resuelto sobre Calorimetría
publicidad
¿Desde qué altura debería caer una determinada masa de agua para que su energía final, convertida en calor, aumente la temperatura de esa masa en 1 °C? Suponga que no haya pérdidas.
Datos: 1 cal = 4,18 J, g = 9,8 m/s2, c = 1 cal/g°C.
Datos del problema:
- Variación de la temperatura del agua: Δ t = 1 °C;
- Calor específico del agua: c = 1 cal/g°C;
- Equivalente mecánico del calor: 1 cal = 4,18 J;
- Aceleración de la gravedad: g = 9,8 m/s2.
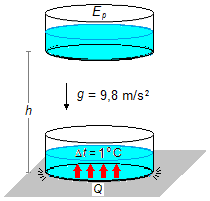
En la posición inicial, a una altura h, toda la energía mecánica de la masa de agua está en forma
de energía potencial EP. Cuando la masa alcanza el suelo, suponiendo que no haya
pérdida de energía, toda la energía potencial se convierte en calor Q que calienta el agua
(Figura 1).
En primer lugar, debemos convertir el calor específico del agua dado en calorías por gramo-grado Celsius (cal/g°C) a julios por kilogramo-grado Celsius (J/kg°C), usado en el Sistema Internacional de Unidades (SI)
\[
\begin{gather}
c=1\;\mathrm{\frac{\cancel{cal}}{\cancel g °C}}\times\frac{4,18\;\mathrm J}{1\;\mathrm{\cancel{cal}}}\times\frac{1000\;\mathrm{\cancel g}}{1\;\mathrm{kg}}=4180\;\mathrm{\frac{J}{kg°C}}
\end{gather}
\]
La Energía Potencial está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_p=mgh} \tag{I}
\end{gather}
\]
La cantidad de calor recibida por el cuerpo está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mc\Delta t} \tag{II}
\end{gather}
\]
La energía potencial inicial se convierte en calor al final, igualando las ecuaciones (I) y (II)
\[
\begin{gather}
E_p=Q \\[5pt]
\cancel m gh=\cancel m c\Delta t \\[5pt]
h=\frac{c \Delta t}{g}
\end{gather}
\]
sustituyendo los datos del problema
\[
\begin{gather}
h=\frac{4180\times 1}{9,8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{h=426,5\;\mathrm m}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .