Exercice Résolu sur les Calorimétrie
publicité
Un corps de masse 200 g est chauffé pendant 30 secondes par une source de chaleur qui fournit une
puissance de 210 W à un taux constant. Étant donné le graphique de la température en fonction du temps,
déterminer la capacité thermique du corps en sachant que 1 cal = 4,2 J.
Données du problème:
- Masse du corps: m = 200 g;
- Puissance de la source de chaleur: \( \mathscr P \) = 210 W.
Premièrement, nous devons convertir l'unité de puissance donnée en watts (joules par seconde) en calories par seconde (cal/s), car dans ce problème, il est plus pratique de ne pas utiliser les unités du Système International d'Unités (SI)
\[
\begin{gather}
\mathscr P=210\;\mathrm W=210\;\mathrm{\frac{J}{s}}=210\;\mathrm{\cancel J}\;\frac{1\;\mathrm{cal}}{4,2\;\mathrm{\cancel J}}\times\frac{1}{\mathrm s}=50\;\mathrm{\frac{cal}{s}}
\end{gather}
\]
La capacité thermique est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{C=mc} \tag{I}
\end{gather}
\]
La quantité de chaleur reçue (ou perdue) est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mc\Delta \theta } \tag{II}
\end{gather}
\]
où θ a été utilisé pour la température au lieu de t, qui a été utilisé pour le temps dans
le problème. En substituant l'équation (I) dans l'équation (II)
\[
\begin{gather}
Q=C \Delta\theta \\[5pt]
C=\frac{Q}{\Delta\theta} \tag{III}
\end{gather}
\]
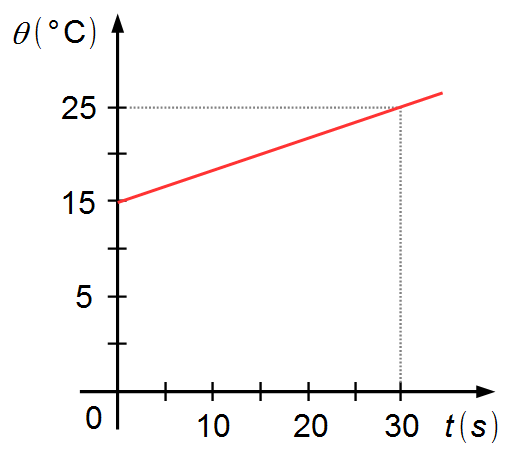
Pendant la période de chauffage, selon le graphique, nous voyons que la température a varié de
\[
\begin{gather}
\Delta\theta=\theta_f-\theta_i \\[5pt]
\Delta\theta=25-15 \\[5pt]
\Delta\theta=10\;\mathrm{°C} \tag{IV}
\end{gather}
\]
La chaleur reçue par le corps est obtenue à partir de la puissance de la source de chaleur. La source fournit
50 calories en 1 seconde, donc en 30 secondes de chauffage, elle va fournir une quantité Q de chaleur.
En utilisant une Règle de Trois
\[
\begin{gather}
\frac{50\;\mathrm{cal}}{1\;\mathrm s}=\frac{Q}{30\;\mathrm s}
\end{gather}
\]
en multipliant en croix
\[
\begin{gather}
(1\;\mathrm s)\times(Q)=(30\;\mathrm s)\times(50\;\mathrm{cal}) \\[5pt]
Q=\frac{(30\;\mathrm{\cancel s})\times(50\;\mathrm{cal})}{1\;\mathrm{\cancel s}} \\[5pt]
Q=1500\;\mathrm{cal} \tag{V}
\end{gather}
\]
en substituant les valeurs (IV) et (V) dans l'équation (III), la capacité thermique sera
\[
\begin{gather}
C=\frac{150\cancel 0}{1\cancel 0}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{C=150\;\mathrm{cal/°C}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .