Ejercicio Resuelto sobre Calorimetría
publicidad
Un cuerpo de masa 200 g se calienta durante 30 segundos por una fuente de calor que suministra una
potencia de 210 W a una tasa constante. Dado el gráfico de la temperatura en función del tiempo,
determine la capacidad térmica del cuerpo, sabiendo que 1 cal = 4,2 J.
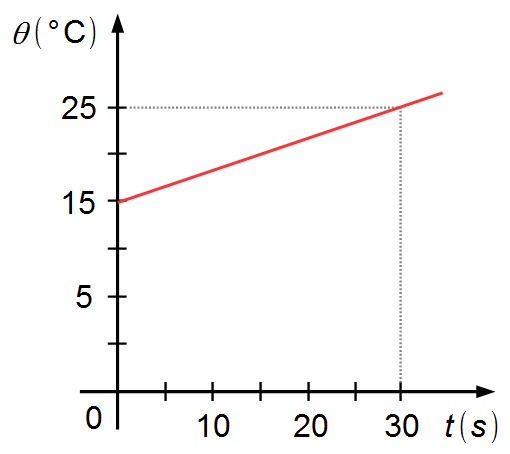
Datos del problema:
- Masa del cuerpo: m = 200 g;
- Potencia de la fuente de calor: \( \mathscr P \) = 210 W.
En primer lugar, debemos convertir la unidad de potencia dada en vatios (joules por segundo) a calorías por segundo (cal/s), ya que en este problema es más conveniente no usar unidades del Sistema Internacional de Unidades (SI)
\[
\begin{gather}
\mathscr P=210\;\mathrm W=210\;\mathrm{\frac{J}{s}}=210\;\mathrm{\cancel J}\;\frac{1\;\mathrm{cal}}{4,2\;\mathrm{\cancel J}}\times\frac{1}{\mathrm s}=50\;\mathrm{\frac{cal}{s}}
\end{gather}
\]
La capacidad térmica se da por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{C=mc} \tag{I}
\end{gather}
\]
La cantidad de calor recibida (o perdida) se da por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mc\Delta \theta } \tag{II}
\end{gather}
\]
donde θ fue usado para la temperatura en lugar de t, que se usó para el tiempo en el
problema. Sustituyendo la ecuación (I) en la ecuación (II)
\[
\begin{gather}
Q=C \Delta\theta \\[5pt]
C=\frac{Q}{\Delta\theta} \tag{III}
\end{gather}
\]
Durante el tiempo de calentamiento, según el gráfico, vemos que la temperatura varió de
\[
\begin{gather}
\Delta\theta=\theta_f-\theta_i \\[5pt]
\Delta\theta=25-15 \\[5pt]
\Delta\theta=10\;\mathrm{°C} \tag{IV}
\end{gather}
\]
El calor recibido por el cuerpo se obtiene a partir de la potencia de la fuente de calor. La fuente
suministra 50 calorías en 1 segundo, así que en los 30 segundos de calentamiento va a suministrar una
cantidad Q de calor, sando una Regla de Tres
\[
\begin{gather}
\frac{50\;\mathrm{cal}}{1\;\mathrm s}=\frac{Q}{30\;\mathrm s}
\end{gather}
\]
multiplicando en cruz
\[
\begin{gather}
(1\;\mathrm s)\times(Q)=(30\;\mathrm s)\times(50\;\mathrm{cal}) \\[5pt]
Q=\frac{(30\;\mathrm{\cancel s})\times(50\;\mathrm{cal})}{1\;\mathrm{\cancel s}} \\[5pt]
Q=1500\;\mathrm{cal} \tag{V}
\end{gather}
\]
sustituyendo los valores (IV) y (V) en la ecuación (III), la capacidad térmica será
\[
\begin{gather}
C=\frac{150\cancel 0}{1\cancel 0}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{C=150\;\mathrm{cal/°C}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .