Exercice Résolu sur les Mouvement Unidimensionnel
publicité
Étant donnée l'équation du mouvement
S = 21 − 10 t + t2
où la position S est mesuré en mètres et le temps t est mesuré en secondes, on demande:
a) Construis un tableau avec des valeurs pour t de 0 à 8 secondes, et à partir du tableau, construis le graphique de la fonction;
b) À quel instant le mobile passe-t-il par l'origine?
c) À quel instant le mobile change-t-il de sens?
Solution
a) Le tableau pour la fonction donnée sera
| t (s) | \( S=21-10t+t^2 \) | \( S(t) \) |
| 0 | \( S(0)=21-10\times 0+0^2 \) | 21 |
| 1 | \( S(1)=21-10\times 1+1^2 \) | 12 |
| 2 | \( S(2)=21-10\times 2+2^2 \) | 5 |
| 3 | \( S(3)=21-10\times 3+3^2 \) | 0 |
| 4 | \( S(4)=21-10\times 4+4^2 \) | − 3 |
| 5 | \( S(5)=21-10\times 5+5^2 \) | − 4 |
| 6 | \( S(6)=21-10\times 6+6^2 \) | − 3 |
| 7 | \( S(7)=21-10\times 7+7^2 \) | 0 |
| 8 | \( S(8)=21-10\times 8+8^2 \) | 5 |
en plaçant les points sur le graphique (Graphique 1)
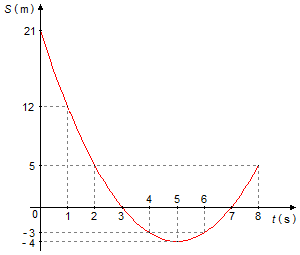
b) Le mobile passe par l'origine lorsque S=0. À partir du tableau et du graphique, nous voyons que cela se produit aux instants t = 3 s et t = 7 s ;
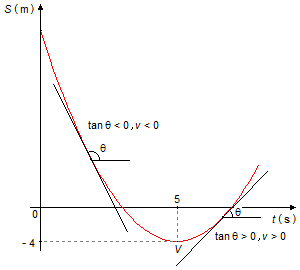
c) Le mobile change de sens lorsque le signe de sa vitesse change. Sur un graphique de la position en fonction du temps, S = f(t), la vitesse est donnée par la tangente au graphique. Sur le Graphique 2, nous voyons que pour les points à gauche du sommet V de la parabole, la tangente est négative (tan θ <0), donc sa vitesse est inférieure à zéro (v < 0). Pour les points à droite du sommet de la parabole, la tangente est positive (tan θ > 0), donc sa vitesse est supérieure à zéro (v>0).
La coordonnée x du sommet d'une parabole est donnée par
\[
\begin{gather}
x=-\frac{b}{2a}
\end{gather}
\]
dans la fonction donnée dans le problème, nous avons a=1 et b=−10, l'instant où le mobile
change de sens est
\[
\begin{gather}
t=-\frac{-10}{2\times 1}
\end {gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=5\;\mathrm s}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .