Exercício Resolvido de Movimento Unidimensional
publicidade
Dada a equação de movimento
S = 21 − 10 t + t2
onde a posição S está medido em metros e o tempo t está medido em segundos, pede-se:
a) Construa uma tabela com valores para t de 0 a 8s, e a partir da tabela construa o gráfico da função;
b) Em que instante o móvel passa pela origem?
c) Em que instante o móvel muda de sentido?
Solução
a) A tabela para a função dada será
| t (s) | \( S=21-10t+t^2 \) | \( S(t) \) |
| 0 | \( S(0)=21-10\times 0+0^2 \) | 21 |
| 1 | \( S(1)=21-10\times 1+1^2 \) | 12 |
| 2 | \( S(2)=21-10\times 2+2^2 \) | 5 |
| 3 | \( S(3)=21-10\times 3+3^2 \) | 0 |
| 4 | \( S(4)=21-10\times 4+4^2 \) | − 3 |
| 5 | \( S(5)=21-10\times 5+5^2 \) | − 4 |
| 6 | \( S(6)=21-10\times 6+6^2 \) | − 3 |
| 7 | \( S(7)=21-10\times 7+7^2 \) | 0 |
| 8 | \( S(8)=21-10\times 8+8^2 \) | 5 |
colocando os pontos no gráfico (Gráfico 1)
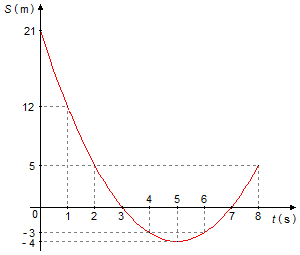
b) O móvel passa pela origem quando S=0, da tabela e do gráfico vemos que isto ocorre nos instantes t = 3 s e t = 7 s ;
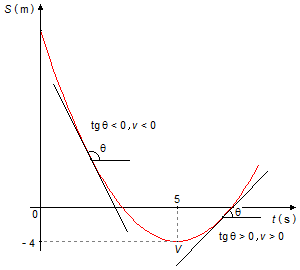
c) O móvel muda de sentido quando muda o sinal de sua velocidade. Em um gráfico da posição em função do tempo, S = f(t), a velocidade é dada pela tangente ao gráfico. Pelo Gráfico 2, vemos que para os pontos à esquerda do vértice V da parábola, a tangente é negativa (tg θ <0), então sua velocidade é menor que zero (v < 0). Para os pontos à direita do vértice da parábola a tangente é positiva (tg θ > 0) então sua velocidade é maior que zero (v>0).
A coordenada x do vértice de uma parábola é dado por
\[
\begin{gather}
x=-\frac{b}{2a}
\end{gather}
\]
na função dada no problema, temos a=1 e b=−10, o instante em que o móvel muda de
sentido é
\[
\begin{gather}
t=-\frac{-10}{2\times 1}
\end {gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=5\;\mathrm s}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .