Ejercicio Resuelto sobre Movimiento Unidimensional

Dada la ecuación de movimiento

S = 21 − 10 t + t²

donde la posición S está medido en metros y el tiempo t está medido en segundos, se pide:
a) Construya una tabla con valores para t de 0 a 8s, y a partir de la tabla construya el gráfico de la función;
b) ¿En qué instante el móvil pasa por el origen?
c) ¿En qué instante el móvil cambia de sentido?

Solución

a) La tabla para la función dada será

t (s)	\( S=21-10t+t^2 \)	\( S(t) \)
0	\( S(0)=21-10\times 0+0^2 \)	21
1	\( S(1)=21-10\times 1+1^2 \)	12
2	\( S(2)=21-10\times 2+2^2 \)	5
3	\( S(3)=21-10\times 3+3^2 \)	0
4	\( S(4)=21-10\times 4+4^2 \)	− 3
5	\( S(5)=21-10\times 5+5^2 \)	− 4
6	\( S(6)=21-10\times 6+6^2 \)	− 3
7	\( S(7)=21-10\times 7+7^2 \)	0
8	\( S(8)=21-10\times 8+8^2 \)	5

poniendo los puntos en el gráfico (Gráfico 1)

Gráfico 1

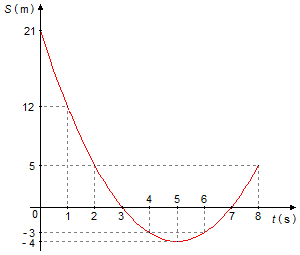
b) El móvil pasa por el origen cuando S=0, de la tabla y del gráfico vemos que esto ocurre en los instantes t = 3 s y t = 7 s ;

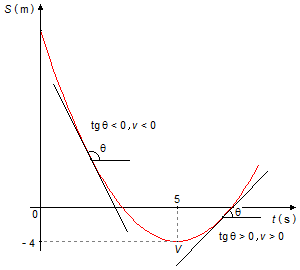
c) El móvil cambia de sentido cuando cambia el signo de su velocidad. En un gráfico de la posición en función del tiempo, S = f(t), la velocidad está dada por la tangente al gráfico. Por el Gráfico 2, vemos que para los puntos a la izquierda del vértice V de la parábola, la tangente es negativa (tg θ <0), entonces su velocidad es menor que cero (v < 0). Para los puntos a la derecha del vértice de la parábola la tangente es positiva (tg θ > 0) entonces su velocidad es mayor que cero (v>0).

La coordenada x del vértice de una parábola está dada por

\[ \begin{gather} x=-\frac{b}{2a} \end{gather} \]

en la función dada en el problema, tenemos a=1 y b=−10, el instante en que el móvil cambia de sentido es

\[ \begin{gather} t=-\frac{-10}{2\times 1} \end {gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {t=5\;\mathrm s} \end{gather} \]

Gráfico 2

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .