Exercice Résolu sur les Dynamique
publicité   



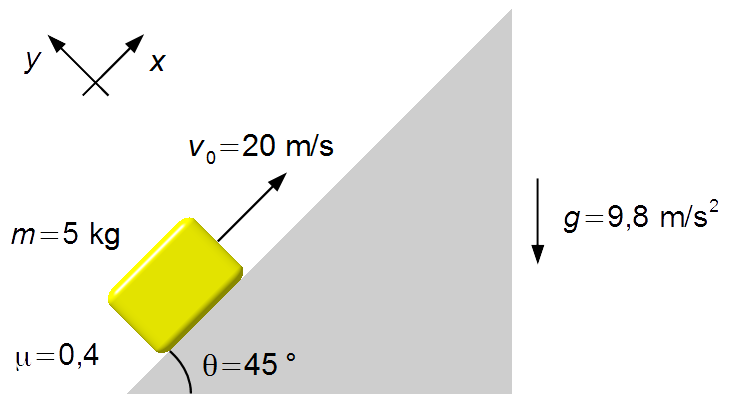
Un bloc, ayant une masse de 5 kg, est lancé avec une vitesse initiale de 20 m/s en direction ascendante sur un plan incliné à 45°. Le coefficient de frottement entre le bloc et le plan est de 0,4. Déterminer la distance que le bloc parcourra avant de s'arrêter.


Données du problème
  • Masse du bloc:    m = 5 kg;
  • Vitesse initiale du bloc:    v0 = 20 m/s;
  • Angle d'inclinaison du plan:    θ = 45°;
  • Coefficient de frottement:    μ = 0,4;
  • Accélération de la pesanteur:    g = 9,8 m/s2.
Schéma du problème

Nous choisissons un référentiel dirigé vers le haut du plan incliné et avec l'axe-x parallèle au plan (Figure 1).

Figure 1

En faisant un Diagramme de Corps Libre, nous avons les forces agissant sur le bloc (Figure 2).
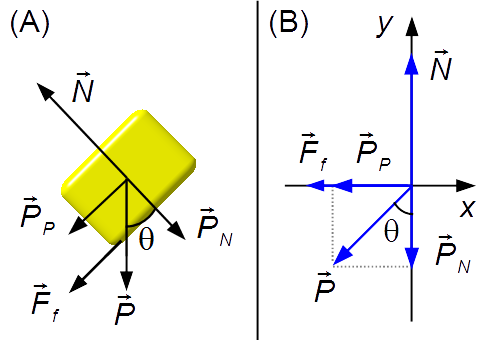
  • \( \vec P \): poids du bloc;
  • \( \vec N \): force de réaction normale de la surface sur le bloc;
  • \( {\vec F}_{f} \): force de frottement entre le bloc et le plan.
Le poids peut être décomposée en deux composantes, une parallèle à l'axe-x, \( {\vec P}_{\small P} \), et l'autre normale ou perpendiculaire, \( {\vec P}_{\small N} \) (Figure 3-A).
Nous dessinons les forces dans un système de coordonnées Oxy (Figure 3-B).
Figure 2

Solution

En appliquant la Deuxième Loi de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Direction x:
\[ \begin{gather} -P_{\small P}-F_{f}=ma \tag{I} \end{gather} \]
La composante parallèle du poids est donnée par
\[ \begin{gather} P_{\small P}=P\sin\theta \tag{II} \end{gather} \]
en substituant l'équation (II) dans l'équation (I)
\[ \begin{gather} -P\sin\theta-F_{f}=ma \tag{III} \end{gather} \]
  • Direction y:
Il n'y a pas de mouvement dans cette direction, la réaction normale et la composante normale du poids s'équilibrent
\[ \begin{gather} N=P_{\small N} \tag{IV} \end{gather} \]
La composante perpendiculaire du poids est donnée par
\[ \begin{gather} P_{\small N}=P\cos \theta \tag{V} \end{gather} \]
en substituant l'équation (V) dans l'équation (IV)
\[ \begin{gather} N=P\cos \theta \tag{VI} \end{gather} \]
Le poids est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{VII} \end{gather} \]
en substituant l'équation (VII) dans les équations (III) et (VI)
\[ \begin{gather} -mg\sin\theta-F_{f}=ma \tag{VIII} \end{gather} \]
\[ \begin{gather} N=mg\cos \theta \tag{IX} \end{gather} \]
La force de frottement est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {{\vec F}_{f}=\mu \vec N} \tag{X} \end{gather} \]
en substituant l'équation (X) dans l'équation (VIII)
\[ \begin{gather} -mg\sin\theta-\mu N=ma \tag{XI} \end{gather} \]
en substituant l'équation (IX) dans l'équation (XI)
\[ \begin{gather} -\cancel{m}g\sin\theta -\mu \cancel{m}g\cos \theta=\cancel{m}a\\[5pt] a=-g(\sin\theta +\mu \cos \theta ) \end{gather} \]
le signe négatif de l'accélération indique qu'elle est opposée à l'orientation de la trajectoire et que le bloc est en train de freiner.
\[ \begin{gather} a=-9,8\times(\sin 45°-0,4\cos 45°) \end{gather} \]

De la trigonométrie, nous avons que   \( \sin 45°=\dfrac{\sqrt{2\;}}{2} \)   et   \( \cos 45°=\dfrac{\sqrt{2\;}}{2} \)

\[ \begin{gather} a=-9,8\times\left(\frac{\sqrt{2\;}}{2}+0,4\times\frac{\sqrt{2\;}}{2}\right)\\[5pt] a=-9,7\;\mathrm{m/s^2} \end{gather} \]
En appliquant l'équation de la vitesse en fonction de l'accélération et du déplacement
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
Le bloc décélère jusqu'à ce que sa vitesse finale soit nulle, v = 0, et en substituant la vitesse initiale donnée dans le problème et l'accélération calculée
\[ \begin{gather} \Delta S=\frac{v^2-v_0^2}{2a}\\[5pt] \Delta S=\frac{0^2-20^2}{2\times\left(-9,7\right)} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta S=20,6\;\mathrm m} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .