Exercício Resolvido de Movimento Unidimensional
publicidade
Um motociclista está em movimento retrógrado, sua velocidade inicial, em módulo, vale 25 m/s e no instante inicial sua posição é de −150 m, a motocicleta está com uma desaceleração, em módulo, de 2 m/s2. Determinar:
a) A função horária do movimento deste motociclista;
b) A função horária da velocidade;
c) O instante em que ele passa pela origem;
d) O instante em que sua velocidade é nula.
Dados do problema:
- Módulo da velocidade inicial do motociclista: |v0| = 25 m/s;
- Módulo da aceleração do motociclista: |a| = 2 m/s2;
- Posição no instante inicial: S0 = −150 m.
Adotamos um sistema de referência com sentido positivo orientado para a direita.
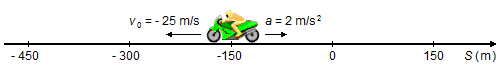
Solução
a) O motociclista possui aceleração, ele está em Movimento Retilíneo Uniformemente Variado (M.R.U.V.), dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}\;t^2}
\end{gather}
\]
o espaço inicial é dado no problema, S0 = −150 m, como o motociclista está em
movimento retrógrado seu movimento se dá contra a orientação da trajetória sendo sua velocidade negativa,
(v<0), temos v = −25 m/s, o motociclista está desacelerando, sua aceleração
está contra a orientação da velocidade (a>0), temos a= 2 m/s2. A função
horária será
\[
\begin{gather}
S=-150-25t+\frac{2}{2}\;t^2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S=-150-25t+t^2}
\end{gather}
\]
b) Para a função horária da velocidade queremos encontrar uma função do tipo
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+at}
\end{gather}
\]
usando os dados do problema obtemos
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=-25t+2t}
\end{gather}
\]
c) Quando o motociclista passa pela origem temos S = 0 substituindo este valor na expressão encontrada no item (a)
\[
\begin{gather}
0=-150-25\;t+t^2
\end{gather}
\]
Esta é uma Equação de 2.º Grau, onde a incógnita é o valor do tempo que queremos encontrar.
Solução da Equação de 2.º Grau
\( t^2-25\;t-150=0 \)
\[
\begin{gather}
\Delta =b^2-4ac=(-25)^2-4\times 1\times(-150)=625+600=1225\\[10pt]
t=\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-(-25)\pm \sqrt{1225\;}}{2\times 1}=\frac{25\pm 35}{2}
\end{gather}
\]
as duas raízes da equação serão
\[
\begin{gather}
t_{1}=30\;\mathrm s\qquad \mathrm{e}\qquad t_2=-5\;\mathrm s
\end{gather}
\]
Como não existe tempo negativo desprezamos a segunda raiz, ele passará pela origem em t = 30 s (ele começa o movimento à esquerda da origem, sua velocidade vai diminuindo devido à desaceleração até ficar igual a zero, então muda de sentido e começa a se mover no sentido do referencial até passar pela origem).
d) Quando a velocidade da moto se anula, temos v = 0, substituindo este valor na expressão encontrada no item (b)
\[
\begin{gather}
0=-25+2t\\[5pt]
2t=25\\[5pt]
t=\frac{25}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=12,5\;\mathrm s}
\end{gather}
\]
Este é o instante que o motociclista muda de sentido e começa a se mover no sentido do referencial até passar
pela origem.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .