Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Un motociclista se mueve en dirección opuesta a la orientación de la trayectoria, su velocidad inicial, en módulo, es de 25 m/s y en el instante inicial su posición es de −150 m, la motocicleta está experimentando una desaceleración, en módulo, de 2 m/s2. Determinar:
a) La ecuación horaria del movimiento de este motociclista;
b) La ecuación horaria de la velocidad;
c) El instante en que pasa por el origen;
d) El instante en que su velocidad es nula.
Datos del problema:
- Módulo de la velocidad inicial del motociclista: |v0| = 25 m/s;
- Módulo de la aceleración del motociclista: |a| = 2 m/s2;
- Posición en el instante inicial: S0 = −150 m.
Tomamos un sistema de referencia con sentido positivo orientado hacia la derecha.
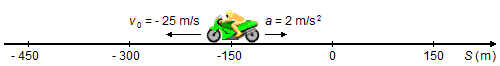
Solución
a) El motociclista tiene una aceleración, está en Movimiento Rectilíneo Uniformemente Variado (MRUV), dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}\;t^2}
\end{gather}
\]
la posición inicial se da en el problema, S0 = −150 m, como el motociclista se mueve
en dirección opuesta a la orientación de la trayectoria, su velocidad es negativa, (v<0), tenemos
v = −25 m/s, el motociclista está desacelerando, su aceleración está en contra de la orientación
de la velocidad (a>0), entonces a= 2 m/s2. La ecuación horaria será
\[
\begin{gather}
S=-150-25t+\frac{2}{2}\;t^2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S=-150-25t+t^2}
\end{gather}
\]
b) Para la ecuación horaria de la velocidad queremos encontrar una función del tipo
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+at}
\end{gather}
\]
Usando los datos del problema, obtenemos
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=-25t+2t}
\end{gather}
\]
c) Cuando el motociclista pasa por el origen, tenemos S = 0. Al sustituir este valor en la expresión encontrada en el ítem (a)
\[
\begin{gather}
0=-150-25\;t+t^2
\end{gather}
\]
Esta es una Ecuación de Segundo Grado, donde la incógnita es el valor del tiempo que queremos
encontrar.
Solución de la Ecuación de Segundo Grado
\( t^2-25\;t-150=0 \)
\[
\begin{gather}
\Delta =b^2-4ac=(-25)^2-4\times 1\times(-150)=625+600=1225\\[10pt]
t=\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-(-25)\pm \sqrt{1225\;}}{2\times 1}=\frac{25\pm 35}{2}
\end{gather}
\]
las dos raíces de la ecuación serán
\[
\begin{gather}
t_{1}=30\;\mathrm s\qquad \mathrm{e}\qquad t_2=-5\;\mathrm s
\end{gather}
\]
Como no existe tiempo negativo, despreciamos la segunda raíz. Pasará por el origen en t = 30 s (comienza el movimiento a la izquierda del origen, su velocidad disminuye debido a la desaceleración hasta llegar a cero, luego cambia de sentido y comienza a moverse en dirección al referencial hasta pasar por el origen).
d) Cuando la velocidad de la moto se anula, tenemos v = 0. Al sustituir este valor en la expresión encontrada en el ítem (b)
\[
\begin{gather}
0=-25+2t\\[5pt]
2t=25\\[5pt]
t=\frac{25}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=12,5\;\mathrm s}
\end{gather}
\]
Este es el instante en que el motociclista cambia de sentido y comienza a moverse en dirección al referencial
hasta pasar por el origen.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .