Exercício Resolvido de Movimento Unidimensional
publicidade   

Um terremoto gera dois tipos de ondas que se propagam pela superfície. As ondas primárias se deslocam com velocidade de 8 km/s e as ondas secundárias se deslocam com velocidade de 5 km/s. Um observador está a uma certa distância do epicentro do terremoto e recebe as ondas primárias e em seguida as ondas secundárias. A que distância do epicentro o observador está se as ondas secundárias chegam depois de 80 s das ondas primárias?

Dados do problema:

  • Velocidade das ondas primárias:    vp = 8 km/s;
  • Velocidade das ondas secundárias:    vs = 5 km/s;
  • Intervalo de tempo entre as ondas primárias e secundárias:    Δt = 80 s.

Esquema do problema:

O problema pode ser reduzido a dois pontos materiais que representam as frentes de onda se movendo com velocidades constantes até passarem pela posição do observador. A onda secundária, mais lenta, passa pelo observador com um atraso de 80 s em relação à onda primária (Figura 1).

Figura 1

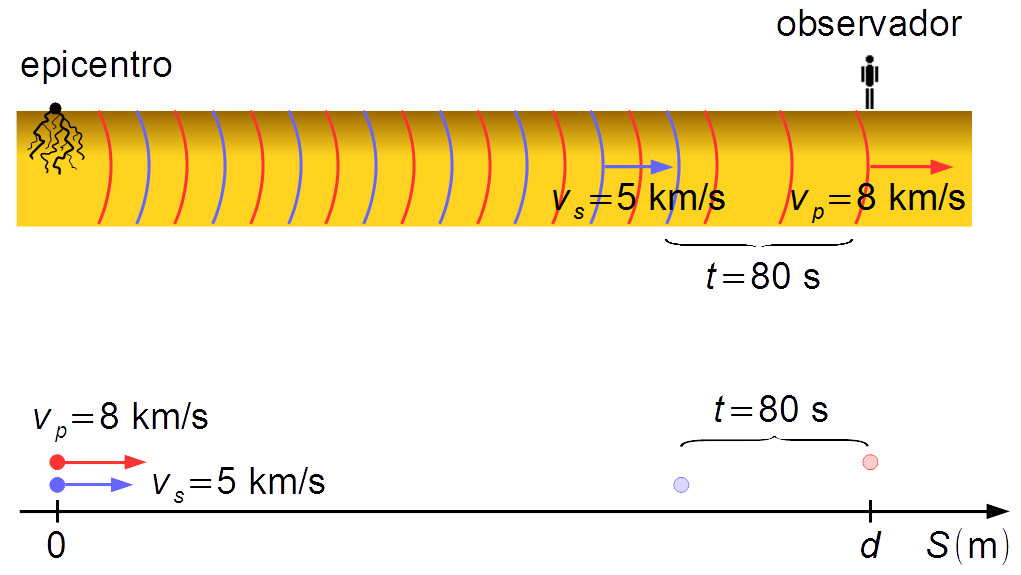
Adotamos um sistema de referência com origem na posição do epicentro do terremoto e orientado para a direita. A posição inicial das partículas é S0p = S0s = 0, a posição final da partícula que representa a onda primária é Sp = d, que é a posição do observador. A partícula que representa a onda secundária possui um atraso de 80 s em relação à primeira partícula.

Solução:

Os dois tipos de ondas se propagam com velocidades constantes, estão em Movimento Retilíneo Uniforme (M.R.U.), dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \\[10pt] S_p=S_{0p}+v_p t_p \tag{I} \\[10pt] S_s=S_{0s}+v_s t_s \tag{II} \end{gather} \]

As ondas primárias atingem o ponto d no instante tp, as ondas secundárias atingem o ponto d 80 s depois

\[ \begin{gather} t_s=t_p+80 \tag{III} \end{gather} \]

Isolando os valores de tp e ts nas equações (I) e (II) e substituindo na equação (III)

\[ \begin{gather} t_p=\frac{d-0}{8} \\[5pt] t_p=\frac{d}{8} \tag{IV} \end{gather} \]
\[ \begin{gather} t_s=\frac{d-0}{5} \\[5pt] t_s=\frac{d}{5} \tag{V} \end{gather} \]
\[ \begin{gather} \frac{d}{5}=\frac{d}{8}+80 \\[5pt] \frac{d}{5}-\frac{d}{8}=80 \end{gather} \]

multiplicando o numerador e o denominador do primeiro termo do lado esquerdo por 8 e o segundo termo por 5

\[ \begin{gather} \frac{8}{8}\times{\frac{d}{5}}-\frac{5}{5}\times{\frac{d}{8}}=80 \\[5pt] \frac{8d}{40}-\frac{5d}{40}=80 \\[5pt] 3d=80\times 40 \\[5pt] d=\frac{3200}{3} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {d\approx 1067\;\mathrm{km}} \end{gather} \]
publicidade