Un terremoto genera dos tipos de ondas que se propagan por la superficie. Las ondas primarias (onda P) se desplazan a una velocidad de 8 km/s y las ondas secundarias (onda S) se desplazan a una velocidad de 5 km/s. Un observador está a cierta distancia del epicentro del terremoto y recibe las ondas primarias y luego las ondas secundarias. ¿A qué distancia del epicentro está el observador si las ondas secundarias llegan después de 80 segundos de las ondas primarias?


Datos del problema:

• Velocidad de las ondas primarias:    v_p = 8 km/s;
• Velocidad de las ondas secundarias:    v_s = 5 km/s;
• Intervalo de tiempo entre las ondas primarias y secundarias:    Δt = 80 s.

Esquema del problema:

El problema se puede reducir a dos puntos materiales que representan los frentes de onda moviéndose con velocidades constantes hasta pasar por la posición del observador. La onda secundaria, más lenta, pasa por el observador con un retraso de 80 segundos en relación con la onda primaria (Figura 1).


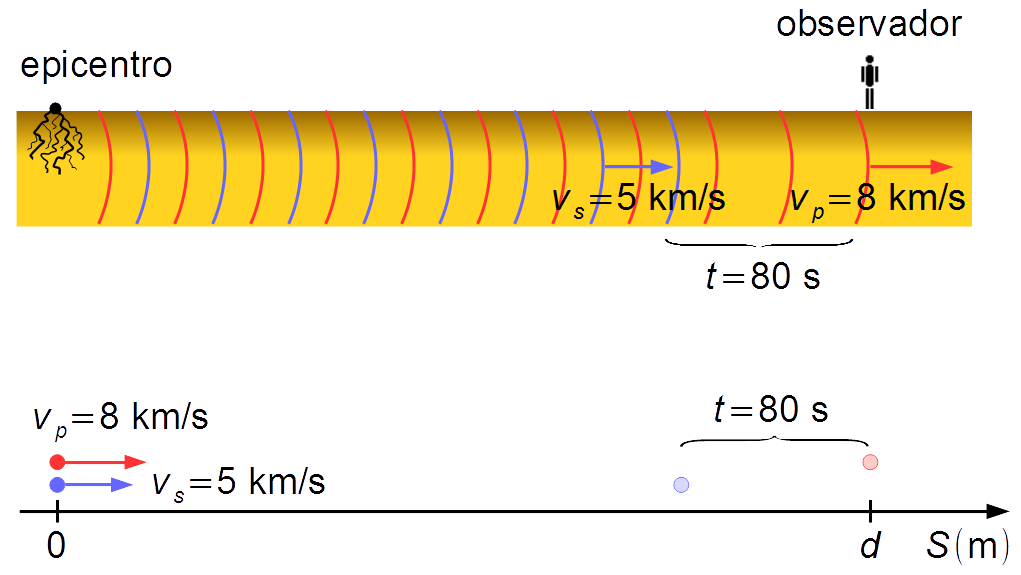
Tomamos un sistema de referencia con origen en la posición del epicentro del terremoto y orientado hacia la derecha. La posición inicial de las partículas es S_0p = S_0s = 0, la posición final de la partícula que representa la onda primaria es S_p = d, que es la posición del observador. La partícula que representa la onda secundaria tiene un retraso de 80 segundos en relación con la primera partícula.

Solución

Los dos tipos de ondas se propagan con velocidades constantes, están en Movimiento Rectilíneo Uniforme (MRU), dado por Las ondas primarias alcanzan el punto d en el instante t_p, las ondas secundarias alcanzan el punto d 80 segundos después Aislando los valores de t_p y t_s en las ecuaciones (I) y (II) y sustituyendo en la ecuación (III) multiplicando el numerador y el denominador del primer término del lado izquierdo por 8 y el segundo término por 5