Un tremblement de terre génère deux types d'ondes qui se propagent à la surface. Les ondes primaires (ondes P) se déplacent à une vitesse de 8 km/s et les ondes secondaires (ondes S) se déplacent à une vitesse de 5 km/s. Un observateur se trouve à une certaine distance de l'épicentre du tremblement de terre et reçoit d'abord les ondes primaires, puis les ondes secondaires. À quelle distance de l'épicentre l'observateur se trouve-t-il si les ondes secondaires arrivent 80 secondes après les ondes primaires?


Données du problème:

• Vitesse des ondes primaires:    v_p = 8 km/s;
• Vitesse des ondes secondaires:    v_s = 5 km/s;
• Intervalle de temps entre les ondes primaires et secondaires:    Δt = 80 s.

Schéma du problème:

Le problème peut être réduit à deux points matériels représentant les fronts d'onde se déplaçant à des vitesses constantes jusqu'à ce qu'ils passent par la position de l'observateur. L'onde secondaire, plus lente, passe par l'observateur avec un retard de 80 s par rapport à l'onde primaire (Figure 1).


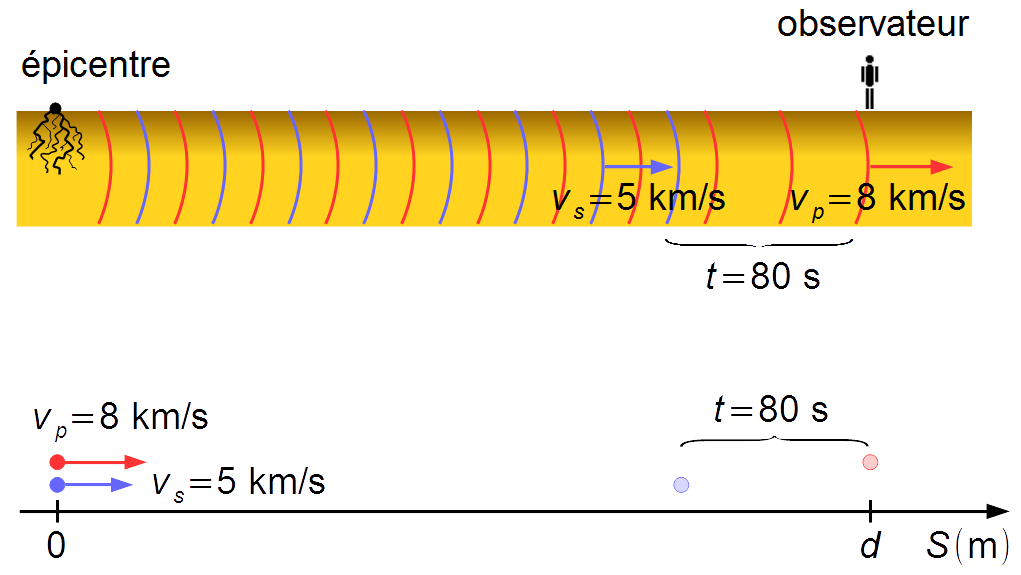
Nous choisissons un référentiel avec une origine à la position de l'épicentre du tremblement de terre et orienté vers la droite. La position initiale des particules est S_0p = S_0s = 0, la position finale de la particule représentant l'onde primaire est S_p = d, qui est la position de l'observateur. La particule représentant l'onde secondaire a un retard de 80 s par rapport à la première particule.

Solution

Les deux types d'ondes se propagent à des vitesses constantes, en Mouvement Rectiligne Uniforme, donné par Les ondes primaires atteignent le point d à l'instant t_p, les ondes secondaires atteignent le point d 80 s plus tard En isolant les valeurs de t_p et t_s dans les équations (I) et (II) et en substituant dans l'équation (III) en multipliant le numérateur et le dénominateur du premier terme du côté gauche par 8 et le deuxième terme par 5