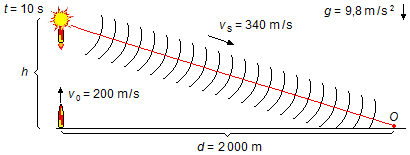
Um foguete é lançado verticalmente, a partir do solo, com velocidade inicial de 200 m/s, após 10 segundos ele explode. Um observador está localizado a uma distância de 2000 metros na mesma horizontal do ponto de lançamento. Depois de quanto tempo o observado ouvirá o barulho da explosão ? A velocidade do som no ar é igual a 340 m/s.

Dados do problema:

• Velocidade inicial do foguete:    v₀ = 200 m/s;
• Intervalo de tempo até a explosão:    t = 10 s;
• Distância do observador ao ponto de lançamento:    d = 2000 m;
• Aceleração da gravidade:    g = 9,8 m/s²;
• Velocidade do som no ar:    v_s = 340 m/s.

Esquema do problema:

O foguete sobe até uma altura h onde explode, o som da explosão viaja pelo ar durante um intervalo de tempo t_s até chegar num observador no solo (Figura 1).

Figura 1

Solução:

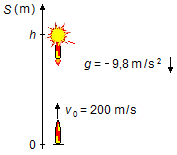
Primeiramente devemos encontrar a altura atingida pelo foguete. Vamos adotar um sistema de referência com origem no solo e orientado para cima (Figura 2).
O movimento do foguete é um lançamento vertical, a altura h da explosão será dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0 t-\frac{g}{2}\;t^2} \end{gather} \]

onde a aceleração da gravidade tem sinal negativo por ter o sentido oposto ao sentido do referencial, sendo S=h e S₀}=0

Figura 2

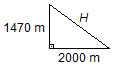
A distância H do ponto da explosão ao observador será dada pelo Teorema de Pitágoras (Figura 3)

\[ \begin{gather} H^2=1470^2+2000^2 \\[5pt] H^2=2160900+4000000 \\[5pt] H^2=6160900 \\[5pt] H=\sqrt{6160900\;} \\[5pt] H\approx 2482\;\mathrm m \end{gather} \]

Figura 3

A onda sonora não sofre ação da gravidade, portanto, ela se movimenta com velocidade constante. O sistema pode ser representado por um ponto da frente de onda em Movimento Retilíneo Uniforme (M.R.U.).
Adotamos um sistema de referência com origem no ponto onde ocorre a explosão orientado para a direita. O ponto se desloca com velocidade constante até onde está o observador (Figura 4)

Figura 4

Sendo S = 2482 m e S₀ = 0, função horária do movimento será dado por