Exercice Résolu sur les Mouvement Unidimensionnel
publicité   



Une fusée est lancée verticalement depuis le sol avec une vitesse initiale de 200 m/s. Après 10 secondes, elle explose. Un observateur au sol situé à une distance de 2000 mètres, sur la même ligne horizontale que le point de lancement. Au bout de combien de temps l’observateur entend-il le bruit de l’explosion? La vitesse du son dans l'air est de 340 m/s.


Données du problème:
  • Vitesse initiale de la fusée:    v0 = 200 m/s;
  • Intervalle de temps jusqu'à l'explosion:    t = 10 s;
  • Distance de l'observateur au point de lancement:    d = 2000 m;
  • Accélération de la pesanteur:    g = 9,8 m/s2;
  • Vitesse du son dans l'air:    vs = 340 m/s.
Schéma du problème:

La fusée monte jusqu'à une hauteur h où elle explose, le son de l'explosion se propage dans l'air pendant un intervalle de temps ts jusqu'à ce qu'il atteigne un observateur au sol (Figure 1).

Figure 1

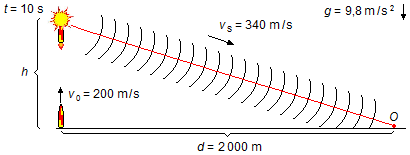
Solution

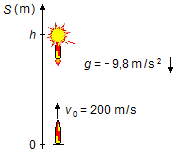
Premièrement, nous devons trouver la hauteur atteinte par la fusée. Nous choisissons un référentiel avec l'origine au sol et orienté vers le haut (Figure 2).
Le mouvement de la fusée est un lancement vertical, la hauteur h de l'explosion sera donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0 t-\frac{g}{2}\;t^2} \end{gather} \]
où l'accélération de la pesanteur a un signe négatif car elle est opposée au sens du référentiel, avec S=h e S0}=0
Figure 2
\[ \begin{gather} h=0+200\times 10-\frac{9,8}{2}\times 10^{2}\\[5pt] h=2000-490\\[5pt] h=1510\;\mathrm m \end{gather} \]
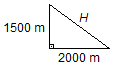
La distance H du point de l'explosion à l'observateur sera donnée par le Théorème de Pythagore (Figure 3)
\[ \begin{gather} H^2=1470^2+2000^2\\[5pt] H^2=2160900+4000000\\[5pt] H^2=6160900\\[5pt] H=\sqrt{6160900\;}\\[5pt] H\approx 2482\;\mathrm m \end{gather} \]
Figure 3

La onde sonore n'est pas soumise à l'action du champ de gravitation, donc elle se déplace avec une vitesse constante. Le système peut être représenté par un point de l'onde avant en Mouvement Rectiligne Uniforme.
Nous choisissons un référentiel avec l'origine au point où l'explosion se produit, orienté vers la droite. Le point se déplace avec une vitesse constante jusqu'à l'observateur (Figure 5)

Figure 5

Étant donné que S = 2482 m et S0 = 0, la fonction horaire du mouvement sera donnée par Sendo S = 2482 m e S0 = 0, função horária do movimento será dado por
\[ \begin{gather} S=S_0+v_{\small S} t_{\small S}\\[5pt] 2482=0+340t_{\small S}\\[5pt] t_{\small S}=\frac{2482}{340} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t_{\small S}\approx 7,3\;\mathrm s} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .