Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad   



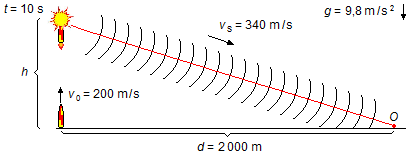
Un cohete es lanzado verticalmente desde el suelo con una velocidad inicial de 200 m/s. Después de 10 segundos, explota. Un observador esta situado a una distancia de 2000 metros en la misma horizontal que el punto de lanzamiento. ¿Después de cuánto tiempo el observador escuchará el sonido de la explosión? La velocidad del sonido en el aire es de 340 m/s.


Datos del problema:
  • Velocidad inicial del cohete:    v0 = 200 m/s;
  • Intervalo de tiempo hasta la explosión:    t = 10 s;
  • Distancia del observador al punto de lanzamiento:    d = 2000 m;
  • Aceleración de la gravedad:    g = 9,8 m/s2;
  • Velocidad del sonido en el aire:    vs = 340 m/s.
Esquema del problema:

El cohete asciende hasta una altura h donde explota, el sonido de la explosión viaja por el aire durante un intervalo de tiempo ts hasta llegar a un observador en el suelo (Figura 1).

Figura 1

Solución

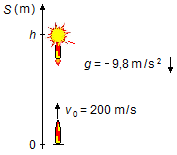
Primero, debemos encontrar la altura alcanzada por el cohete. Tomamos un sistema de referencia con origen en el suelo y orientado hacia arriba (Figura 2).
El movimiento del cohete es un lanzamiento vertical, la altura h de la explosión será dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0 t-\frac{g}{2}\;t^2} \end{gather} \]
donde la aceleración de la gravedad tiene signo negativo por tener el sentido opuesto al sentido del referencial, siendo S=h e S0}=0
Figura 2
\[ \begin{gather} h=0+200\times 10-\frac{9,8}{2}\times 10^{2}\\[5pt] h=2000-490\\[5pt] h=1510\;\mathrm m \end{gather} \]
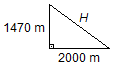
La distancia H desde el punto de la explosión hasta el observador será dada por el Teorema de Pitágoras (Figura 3)
\[ \begin{gather} H^2=1470^2+2000^2\\[5pt] H^2=2160900+4000000\\[5pt] H^2=6160900\\[5pt] H=\sqrt{6160900\;}\\[5pt] H\approx 2482\;\mathrm m \end{gather} \]
Figura 3

La onda sonora no sufre la acción de la gravedad, por lo tanto, se mueve con velocidad constante. El sistema puede ser representado por un punto del frente de onda en Movimiento Rectilíneo Uniforme (MRU).
Tomamos un sistema de referencia con origen en el punto donde ocurre la explosión orientado hacia la derecha. El punto se desplaza con velocidad constante hasta donde está el observador (Figura 5)

Figura 5

Siendo S = 2482 m y S0 = 0, la función horaria del movimiento será dada por
\[ \begin{gather} S=S_0+v_{\small S} t_{\small S}\\[5pt] 2482=0+340t_{\small S}\\[5pt] t_{\small S}=\frac{2482}{340} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t_{\small S}\approx 7,3\;\mathrm s} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .