Exercício Resolvido de Movimento Unidimensional
publicidade
Um móvel parte com velocidade inicial de 1 m/s em movimento retilíneo, é dado o gráfico da aceleração em função do tempo a partir do início do movimento
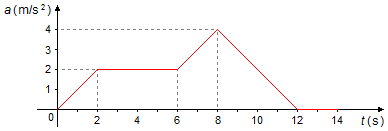
Determinar:
a) A velocidade em t = 8 s;
b) A velocidade em t = 12 s;
c) A velocidade em t = 14 s;
d) Entre que intervalo de tempo a velocidade diminui.
Dado do problema:
- Velocidade inicial do móvel: v0 = 1 m/s.
a) Em um gráfico da aceleração em função do tempo, a = f(t), a variação da velocidade é igual a área sob a curva.
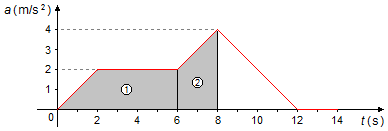
Podemos dividir o gráfico nas seguintes áreas (Figura 1):
- Entre os instantes 0 s e 6 s, um trapézio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{[6+(6-2)]\times 2}{2}\\[5pt]
A_1=\frac{[6+4]\times 2}{2}\\[5pt]
A_1=\frac{10\times 2}{2}\\[5pt]
A_1=10
\end{gather}
\]
- Entre os instantes 6 s e 8 s, um trapézio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4+2)\times(8-6)}{2}\\[5pt]
A_2=\frac{6\times2}{2}\\[5pt]
A_2=6
\end{gather}
\]
A variação da velocidade será a área total dada pela soma das áreas encontradas
\[
\begin{gather}
\Delta v=A_1+A_2\\[5pt]
\Delta v=10+6\\[5pt]
\Delta v=16\;\mathrm{m/s}
\end{gather}
\]
Da definição de variação da velocidade
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta v=|\;v_f-v_i\;|} \tag{I}
\end{gather}
\]
usando a variação da velocidade encontrada acima e a velocidade inicial dada no problema
(vi = v0 = 1 m/s), a velocidade em t = 8 s será
\[
\begin{gather}
16=|\;v_8-1\;|\\[5pt]
16=v_8-1\\[5pt]
v_8=16+1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_8=17\;\mathrm{m/s}}
\end{gather}
\]
b) Para encontrar a velocidade em t = 12 s devemos encontrar a variação da velocidade entre t = 8 s e t = 12 s (Figura 2).
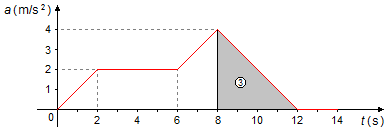
- Entre os instantes 8 s e 12 s, temos um triângulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(12-8)\times 4}{2}\\[5pt]
A_3=\frac{4\times 4}{2}\\[5pt]
A_3=8
\end{gather}
\]
Sendo esta área igual a variação da velocidade (Δv) e a velocidade encontrada no item (a) como
sendo a velocidade inicial desta parte do movimento (vi = v8 = 17 m/s),
a expressão (I) nos dá
\[
\begin{gather}
8=|\;v_{\;12}-17\;|\\[5pt]
8=v_{12}-17\\[5pt]
v_{12}=8+17
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_{12}=25\;\mathrm{m/s}}
\end{gather}
\]
c) Entre 12 s e 14 s a aceleração é nula (a = 0, portanto não há mudança na velocidade do móvel, sua velocidade permanece constante.
d) A velocidade não diminui em nenhum intervalo de tempo.
Observação: entre os instantes 8 s e 12 s, o gráfico apresenta uma reta em que a aceleração
diminui com o tempo. Mas isto não significa que a velocidade diminua, a reta está acima do eixo das
abscissas (eixo do tempo) assim a aceleração tem valor positivo (a>0) e a velocidade aumenta em
uma taxa menor. Para que a velocidade diminuísse seria necessário que a reta estivesse abaixo do eixo das
abscissas, a aceleração teria valor negativo (a<0) e o móvel estaria sendo freado.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .