Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Un objeto parte con una velocidad inicial de 1 m/s en movimiento rectilíneo, se proporciona el gráfico de la aceleración en función del tiempo desde el inicio del movimiento.
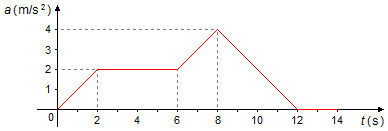
Determinar:
a) La velocidad en t = 8 s;
b) La velocidad en t = 12 s;
c) La velocidad en t = 14 s;
d) En qué intervalo de tiempo la velocidad disminuye.
Datos del problema:
- Velocidad inicial del objeto: v0 = 1 m/s.
a) En un gráfico de aceleración en función del tiempo, a = f(t), la variación de velocidad es igual al área bajo la curva.
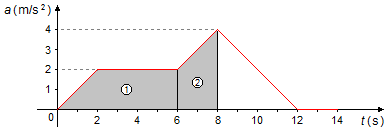
Podemos dividir el gráfico en las siguientes áreas (Figura 1):
- Entre los instantes 0 s y 6 s, un trapecio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{[6+(6-2)]\times 2}{2}\\[5pt]
A_1=\frac{[6+4]\times 2}{2}\\[5pt]
A_1=\frac{10\times 2}{2}\\[5pt]
A_1=10
\end{gather}
\]
- Entre los instantes 6 s y 8 s, un trapecio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4+2)\times(8-6)}{2}\\[5pt]
A_2=\frac{6\times2}{2}\\[5pt]
A_2=6
\end{gather}
\]
La variación de velocidad será el área total dada por la suma de las áreas encontradas
\[
\begin{gather}
\Delta v=A_1+A_2\\[5pt]
\Delta v=10+6\\[5pt]
\Delta v=16\;\mathrm{m/s}
\end{gather}
\]
De la definición de variación de velocidad
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta v=|\;v_f-v_i\;|} \tag{I}
\end{gather}
\]
usando la variación de velocidad encontrada arriba y la velocidad inicial dada en el problema
(vi = v0 = 1 m/s), la velocidad en t = 8 s será
\[
\begin{gather}
16=|\;v_8-1\;|\\[5pt]
16=v_8-1\\[5pt]
v_8=16+1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_8=17\;\mathrm{m/s}}
\end{gather}
\]
b) Para encontrar la velocidad en t = 12 s, debemos encontrar la variación de velocidad entre t = 8 s y t = 12 s (Figura 2).
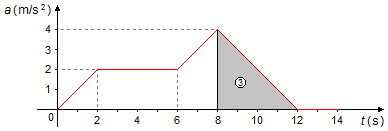
- Entre los instantes 8 s y 12 s, tenemos un triángulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(12-8)\times 4}{2}\\[5pt]
A_3=\frac{4\times 4}{2}\\[5pt]
A_3=8
\end{gather}
\]
Siendo esta área igual a la variación de velocidad (Δv) y la velocidad encontrada en el ítem (a)
como la velocidad inicial de esta parte del movimiento
(vi = v8 = 17 m/s), la expresión (I) nos da
\[
\begin{gather}
8=|\;v_{\;12}-17\;|\\[5pt]
8=v_{12}-17\\[5pt]
v_{12}=8+17
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_{12}=25\;\mathrm{m/s}}
\end{gather}
\]
c) Entre 12 s y 14 s , la aceleración es nula (a = 0), por lo tanto, no hay cambio en la velocidad del objeto, su velocidad permanece constante.
d) La velocidad no disminuye en ningún intervalo de tiempo.
Observación: entre los instantes 8 s y 12 s, el gráfico muestra una línea en la que la
aceleración disminuye con el tiempo. Pero esto no significa que la velocidad disminuya, la línea está por
encima del eje de las abscisas (eje del tiempo), por lo que la aceleración tiene un valor positivo
(a>0) y la velocidad aumenta a una tasa menor. Para que la velocidad disminuyera, sería necesario
que la línea estuviera por debajo del eje de las abscisas, la aceleración tendría un valor negativo
(a<0) y el objeto estaría siendo frenado.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .