Exercice Résolu sur les Mouvement Unidimensionnel
publicité
Un objet démarre avec une vitesse initiale de 1 m/s en mouvement rectiligne, le graphique de l'accélération en fonction du temps depuis le début du mouvement est donné
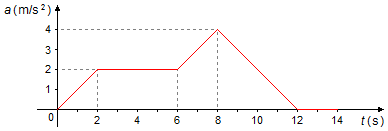
Déterminer:
a) La vitesse à t = 8 s;
b) La vitesse à t = 12 s;
c) La vitesse à t = 14 s;
d) Pendant quel intervalle de temps la vitesse diminue.
Donnée du problème:
- Vitesse initiale de l'objet: v0 = 1 m/s.
a) Sur un graphique de l'accélération en fonction du temps, a = f(t), la variation de la vitesse est égale à l'aire sous la courbe.
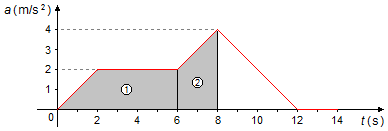
Nous pouvons diviser le graphique en les aires suivantes (Figure 1):
- Entre les instants 0 s et 6 s, un trapèze d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{[6+(6-2)]\times 2}{2}\\[5pt]
A_1=\frac{[6+4]\times 2}{2}\\[5pt]
A_1=\frac{10\times 2}{2}\\[5pt]
A_1=10
\end{gather}
\]
- Entre les instants 6 s et 8 s, un trapèze d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4+2)\times(8-6)}{2}\\[5pt]
A_2=\frac{6\times2}{2}\\[5pt]
A_2=6
\end{gather}
\]
La variation de la vitesse sera l'aire totale donnée par la somme des aires trouvées
\[
\begin{gather}
\Delta v=A_1+A_2\\[5pt]
\Delta v=10+6\\[5pt]
\Delta v=16\;\mathrm{m/s}
\end{gather}
\]
À partir de la définition de la variation de la vitesse
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta v=|\;v_f-v_i\;|} \tag{I}
\end{gather}
\]
en utilisant la variation de vitesse trouvée ci-dessus et la vitesse initiale donnée dans le problème
(vi = v0 = 1 m/s), la vitesse à t = 8 s sera
\[
\begin{gather}
16=|\;v_8-1\;|\\[5pt]
16=v_8-1\\[5pt]
v_8=16+1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_8=17\;\mathrm{m/s}}
\end{gather}
\]
b) Pour trouver la vitesse à t = 12 s, nous devons trouver la variation de vitesse entre t = 8 s et t = 12 s (Figure 2).
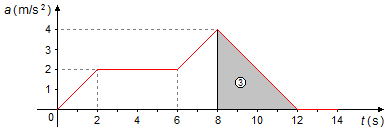
- Entre les instants 8 s et 12 s, nous avons un triangle d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(12-8)\times 4}{2}\\[5pt]
A_3=\frac{4\times 4}{2}\\[5pt]
A_3=8
\end{gather}
\]
Cette aire étant égale à la variation de vitesse (Δv) et la vitesse trouvée à l'article (a)
étant la vitesse initiale de cette partie du mouvement
(vi = v8 = 17 m/s), l'expression (I) nous donne
\[
\begin{gather}
8=|\;v_{\;12}-17\;|\\[5pt]
8=v_{12}-17\\[5pt]
v_{12}=8+17
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_{12}=25\;\mathrm{m/s}}
\end{gather}
\]
c) Entre 12 s et 14 s l'accélération est nulle (a = 0), donc il n'y a aucun changement dans la vitesse de l'objet, sa vitesse reste constante.
d) La vitesse ne diminue dans aucun intervalle de temps.
Remarque: entre les instants 8 s et 12 s, le graphique présente une ligne où l'accélération
diminue avec le temps. Cependant, cela ne signifie pas que la vitesse diminue, la ligne est au-dessus de
l'axe des abscisses (axe du temps), donc l'accélération a une valeur positive (a>0) et la vitesse
augmente à un rythme moindre. Pour que la vitesse diminue, il faudrait que la ligne soit en dessous de
l'axe des abscisses, l'accélération aurait une valeur négative (a<0) et l'objet serait freiné.
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .