Exercício Resolvido de Movimento Unidimensional
publicidade
O movimento de um corpo é dado pelo gráfico da velocidade em função do tempo, v = f(t):

Determinar:
a) O espaço percorrido entre 1 s e 9 s;
b) A velocidade média entre 1 s e 9 s;
c) A aceleração média entre 1 s e 9 s.
Solução
a) Em um gráfico da velocidade em função do tempo, v = f(t) o espaço percorrido é igual a área sob a curva. O eixo das abscissas (eixo do tempo) está dividido em unidade de 1 s, o eixo das ordenadas (eixo da velocidade) está dividido em unidades de 1 m/s. A área de um quadrado é a multiplicação dos lados
\[
\begin{gather}
1\;\cancel{\mathrm s}\times 1\;\frac{\mathrm m}{\cancel{\mathrm s}}=1\;\mathrm m
\end{gather}
\]
um quadrado do gráfico representa 1 m de deslocamento do móvel.
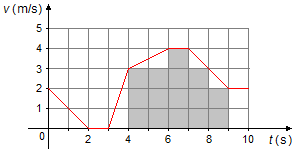
Entre os instantes 4 s e 9 s, temos por contagem direta, 15 quadrados que representam 15 m de deslocamento
(Figura 1)
\[
\begin{gather}
A_{1}=15\;\mathrm m
\end{gather}
\]
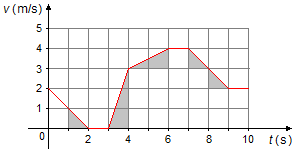
Da Figura 2 vemos que entre 1 s e 2 s temos meio quadrado o que representa 0,5 m de deslocamento
\[
\begin{gather}
A_{2}=0,5\;\mathrm m
\end{gather}
\]
Entre 3 s e 4 s as áreas entre as velocidades 0 e 1 m/s e entre 2 m/s e 3 m/s se completam de modo a
formar um quadrado e o deslocamento será de 1 m
\[
\begin{gather}
A_{3}=1\;\mathrm m
\end{gather}
\]
entre as velocidades de 1 m/s e 2 m/s, temos meio quadrado o que representa 0,5 m de deslocamento
\[
\begin{gather}
A_{4}=0,5\;\mathrm m
\end{gather}
\]
Entre 4 s e 6 s as áreas completam de modo a formar um quadrado e o deslocamento será de 1 m
\[
\begin{gather}
A_{5}=1\;\mathrm m
\end{gather}
\]
Entre 7 s e 9 s temos duas meias áreas que se completam de modo a formar um quadrado e o deslocamento será de
1 m
\[
\begin{gather}
A_{6}=1\;\mathrm m
\end{gather}
\]
O espaço percorrido será a área total dada pela soma das áreas encontradas
\[
\begin{gather}
\Delta S=A_{1}+A_{2}+A_{3}+A_{4}+A_{5}+A_{6}\\[5pt]
\Delta S=15+0,5+1+0,5+1+1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=19\;\mathrm m}
\end{gather}
\]
b) A velocidade média é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_m=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
usando o espaço percorrido encontrado no item (a)
\[
\begin{gather}
v_m=\frac{19}{9-1}\\[5pt]
v_m=\frac{19}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_m\approx 2,4\;\mathrm{m/s}}
\end{gather}
\]
c) A aceleração média é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_m=\frac{\Delta v}{\Delta t}}
\end{gather}
\]
do gráfico temos que para t1 = 1 s a velocidade vale v1 = 1 m/s, e para
t2 = 9 s a velocidade vale v2 = 2 m/s
\[
\begin{gather}
a_m=\frac{2-1}{9-1}\\[5pt]
a_m=\frac{1}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_m\approx 0,1\;\mathrm{m/s^2}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .