Ejercicio Resuelto sobre Movimiento Bidimensional
publicidad
Una pelota rueda sobre una mesa horizontal de altura H, con velocidad constante v0, sin fricción, hasta que cae por el borde. Calcule:
a) El tiempo necesario para que la pelota alcance el suelo;
b) La distancia horizontal, desde el borde de la mesa, donde la pelota golpea el suelo;
c) La ecuación de la trayectoria del movimiento;
d) La velocidad con la que la pelota golpea el suelo.
Datos del problema:
- Velocidad inicial de la bola sobre la mesa: v0;
- Altura de la mesa: H.
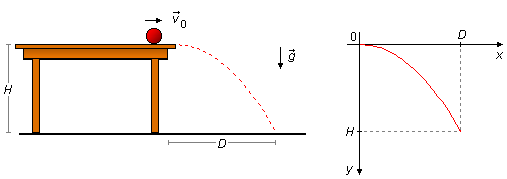
Tomamos un sistema de referencia en la mesa con el eje Ox apuntando hacia la derecha y Oy hacia abajo, la aceleración de la gravedad está dirigida hacia abajo y el punto desde donde la bola cae de la mesa está en (x0, y0) = (0, 0) (Figura 1).
Solución
El movimiento puede ser proyectado en las direcciones x e y. La velocidad inicial v0, con la que la bola rueda sobre la mesa en la dirección x, será la única velocidad hasta el momento en que la bola cae por el borde de la mesa, en la dirección y la velocidad inicial será nula
\[
\begin{gather}
v_{0 x} = v_0 \tag{I}\\[10pt]
v_{0 y} = 0 \tag{II}
\end{gather}
\]
Proyectando el movimiento, en la dirección x no hay aceleración actuando sobre la bola, está en
Movimiento Rectilíneo Uniforme (MRU) y su movimiento es dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_x=S_{0x}+v_xt}
\end{gather}
\]
como en el movimiento uniforme vx = v0x es constante, podemos
substituir vx por el valor de (I) y S0x = 0
\[
\begin{gather}
S_x=0+v_0t\\[5pt]
S_x=v_0t \tag{III}
\end{gather}
\]
En la dirección y la bola está bajo la acción de la aceleración de la gravedad, por lo tanto está en
caída libre dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_y=S_{0y}+v_{0y}t+\frac{g}{2}t^2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_y=v_{0y}+gt}
\end{gather}
\]
sustituyendo v0y por el valor dado en (II) y S0y = 0
\[
\begin{gather}
S_y=0+0\times t+\frac{g}{2}t^2\\[5pt]
S_y=\frac{g}{2}t^2 \tag{IV}
\end{gather}
\]
\[
\begin{gather}
v_y=gt \tag{V}
\end{gather}
\]
con g constante (el signo positivo indica que la aceleración de la gravedad está en la misma
dirección que la orientación del sistema de referencia).
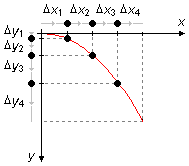
En la Figura 2 vemos que en el movimiento a lo largo de la dirección x tenemos que, para
intervalos de tiempos iguales tenemos intervalos de desplazamientos iguales
(Δx1 = Δx2 =
Δx3 = Δx4). En la dirección y tenemos que, en el
instante que la bola cae de la mesa la velocidad vy comienza a aumentar a partir de
cero bajo la acción de la gravedad, para intervalos de tiempos iguales tenemos intervalos de
desplazamientos cada vez mayores
(Δ1 < Δ2 < Δ3 <
Δ4).
a) El intervalo de tiempo para que la bola alcance el suelo se obtendrá de la ecuación (IV) con la condición de que en el suelo la altura de caída sea la altura de la mesa, Sy = H
\[
\begin{gather}
H=\frac{g}{2}t^2\\[5pt]
t^2=\frac{2H}{g}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=\sqrt{\frac{2H}{g}\;}}
\end{gather}
\]
b) El intervalo de tiempo calculado anteriormente, para que la bola caiga hasta el suelo, también es el intervalo de tiempo que tomará para ir desde el origen hasta el punto D a lo largo del eje x, sustituyendo la respuesta del ítem anterior en la expresión (III).
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{D=v_0\sqrt{\frac{2H}{g}\;}}
\end{gather}
\]
c) Para obtener la ecuación de la trayectoria (Figura 1), debemos tener y como función de x, o y = f(x), utilizando las ecuaciones (III) y (IV) para los movimientos en x e y. Aislamos el tiempo en la expresión (III)
\[
\begin{gather}
t=\frac{S_x}{v_0}
\end{gather}
\]
sustituyendo este valor en la ecuación (IV)
\[
\begin{gather}
S_y=\frac{g}{2}\left(\frac{S_x}{v_0}\right)^2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_y={\frac{g}{2v_0^2}S_x^2}}
\end{gather}
\]
Al hacer la asociación con una Ecuación del Segundo Grado del tipo
y = ax2+bx+c
\[
\begin{array}{c}
S_y & = & {\dfrac{g}{2v_0^2}} & S_x^2 & + & 0 & S_x & + & 0\\
\downarrow & & \downarrow & \downarrow & & \downarrow & \downarrow & & \downarrow \\
y & = & a & x^2 & + & b & x & + & c
\end{array}
\]
vemos que hemos obtenido una función del tipo Sy = f(Sx) con el
coeficiente a > 0, lo que indica que la trayectoria es una parábola con la "boca" apuntando en la
misma dirección del eje y positivo (en este caso hacia abajo, contrario a lo que usualmente sucede).
d) Cuando la bola alcanza el suelo, su velocidad tiene componentes en las direcciones x e y (Figura 3). La velocidad en la dirección x está dada por la expresión (I) y la velocidad en la dirección y se obtiene de la expresión (V) donde se sustituye el tiempo por el valor encontrado en el ítem (a)
\[
\begin{gather}
v_y=g\sqrt{\frac{2H}{g}\;}\\[5pt]
v_y=\sqrt{\frac{2Hg^{\cancel 2}}{\cancel g}\;}\\[5pt]
v_y=\sqrt{2gH\;}
\end{gather}
\]
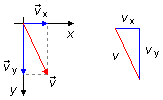
La velocidad de la bola será dada por la suma vectorial
\[
\begin{gather}
\vec v={\vec v}_x+{\vec v}_y
\end{gather}
\]
El módulo se obtiene aplicando el Teorema de Pitágoras
\[
\begin{gather}
v^2=v_x^2+v_y^2\\[5pt]
v^2=v_0^2+\left(\sqrt{2gH}\right)^2\\[5pt]
v^2=v_0^2+2gH
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=\sqrt{v_0^2+2gH\;}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .