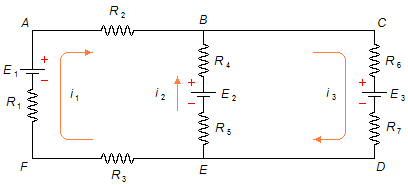
En el circuito siguiente, determinar las corrientes en las ramas y sus verdaderos sentidos.

 

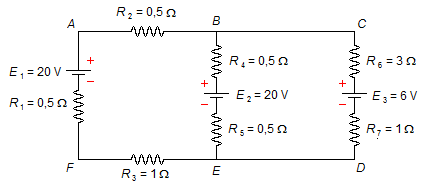
Datos del problema:

Resistores:

• R₁ = 0,5 Ω;
• R₂ = 0,5 Ω;
• R₃ = 1 Ω;
• R₄ = 0,5 Ω;
• R₅ = 0,5 Ω;
• R₆ = 3 Ω;
• R₇ = 1 Ω.

Baterías:

• E₁ = 20 V;
• E₂ = 20 V;
• E₃ = 6 V;

Solución:

En primer lugar, a cada malla del circuito le asignamos, aleatoriamente, un sentido de corriente. En la malla ABEFA tenemos la corriente i₁ en sentido horario y en la malla BCDEB tenemos la corriente i₂ también en sentido horario (Figura 1)

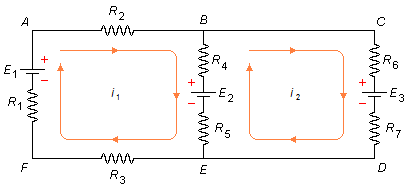
Aplicando la Segunda Ley de Kirchhoff a la malla i₁ a partir del punto A en el sentido elegido, ignorando la malla i₂ (Figura 2)

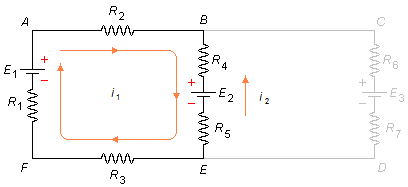
sustituyendo los valores del problema

Ignorando la malla i₁ y aplicando la Segunda Ley de Kirchhoff a la malla i₂, tenemos, según la Figura 3, a partir del punto B

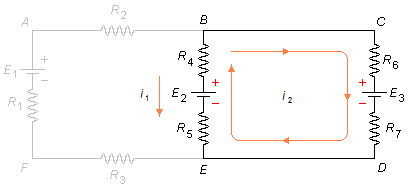
sustituyendo los valores del problema

Con las ecuaciones (I) y (II) tenemos un sistema de dos ecuaciones con dos incógnitas (i₁ e i₂)

Aislando el valor de i₂ en la primera ecuación

sustituyendo este valor en la segunda ecuación

Sustituyendo este valor en la ecuación (III)

En la rama BE circulará una corriente i₃ dada por

El sentido de la corriente i₃ será el mismo que el de la corriente i₂ (de mayor valor).
Como los valores de las corrientes son todos positivos, esto indica que los sentidos elegidos en la Figura 1 son correctos. Los valores de las corrientes son i₁=1 A, i₂=2 A, e i₃=3 A, y sus sentidos están mostrados en la Figura 4.