Ejercicio Resuelto sobre Calorimetría
publicidad
Una licuadora, cuyo motor tiene una potencia de 84 W, se utiliza para agitar 100 g de agua durante 30 segundos. Se supone que todo el trabajo del motor se transfiere en forma de calor al agua dentro de la licuadora y que no hay otras transferencias de energía. Calcule el calentamiento de la masa de agua. Dado: 1 cal = 4,2 J.
Datos del problema:
- Potencia de la licuadora: \( {\mathscr P} = 84 W \);
- Masa de agua: m = 100 g;
- Intervalo de tiempo: Δt = 30 s;
- Calor específico del agua: c = 1 cal/g°C;
- Equivalente mecánico del calor: 1 cal = 4,2 J.
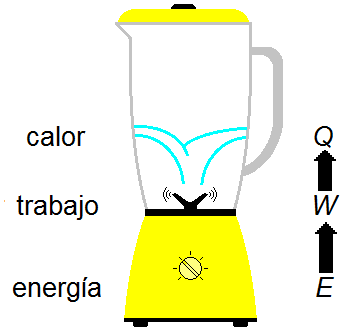
Toda la energía E producida por el motor se utiliza en el trabajo W para producir calor
Q que calienta el agua (Figura 1).
\[
\begin{gather}
E=W=Q
\end{gather}
\]
Solución:
La potencia suministrada por la licuadora durante el tiempo de funcionamiento se expresa como
\[
\begin{gather}
\bbox[#99CCFF,10px]
{{\mathscr P}=\frac{E}{\Delta t}}
\end{gather}
\]
\[
\begin{gather}
E=\mathscr P\Delta t \\[5pt]
E=84\times 30 \\[5pt]
E=2520\;\mathrm J
\end{gather}
\]
Convirtiendo la energía calculada en julios (J) a calorías (cal) utilizada en el problema
\[
\begin{gather}
E=2520\;\mathrm{\cancel J}\times\frac{1\;\mathrm{cal}}{4,2\;\mathrm{\cancel J}}=600\;\mathrm{cal}
\end{gather}
\]
\[
\begin{gather}
E=Q=600\;\mathrm{cal}
\end{gather}
\]
La ecuación de calor está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mc\Delta\theta}
\end{gather}
\]
\[
\begin{gather}
\Delta \theta=\frac{Q}{mc} \\[5pt]
\Delta \theta=\frac{600}{100\times 1}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta \theta =6\;\mathrm{°C}}
\end{gather}
\]
Observación: para la temperatura se utilizó el símbolo θ para no confundir con
t usado para el intervalo de tiempo en la fórmula de la potencia.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .