Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad   



Un trabajador sale de su casa y camina 600 metros en 5 minutos hasta la parada de autobús. Tan pronto como llega a la parada, toma el autobús y viaja durante 40 minutos a una velocidad constante de 18 kilómetros por hora hasta la fábrica donde trabaja. Si él hiciera todo el trayecto en bicicleta, a una velocidad constante de 6 metros por segundo. ¿Cuánto tiempo le llevaría desde su casa hasta la fábrica? Proporcione la respuesta en minutos.


Datos del problema:
  • Distancia de la casa a la parada de autobús:    ΔS1 = 600 m;
  • Tiempo transcurrido desde la casa hasta la parada de autobús:    Δt1 = 5 min;
  • Tiempo transcurrido desde la parada de autobús hasta la fábrica:    Δt2 = 40 min;
  • Velocidad del autobús:    vo = 18 km/h;
  • Velocidad de la bicicleta:    v3 = 6 m/s.
Esquema del problema:

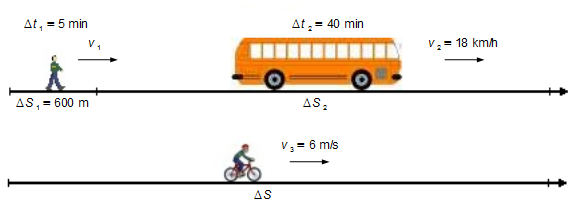
Tomamos un sistema de referencia orientado hacia la derecha (Figura 1)

Figura 1

Solución

Convirtiendo los intervalos de tiempo dados en minutos a segundos y la velocidad del autobús dada en kilómetros por hora a metros por segundo, utilizando el Sistema Internacional de Unidades (SI)
\[ \begin{gather} \Delta t_1=5\;\cancel{\mathrm{min}}\times\frac{60\;\mathrm s}{1\;\cancel{\mathrm{min}}}=300\;\mathrm s\\[10pt] \Delta t_2=40\;\cancel{\mathrm{min}}\times\frac{60\;\mathrm s}{1\;\cancel{\mathrm{min}}}=2400\;\mathrm s\\[10pt] v_2=18\;\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{18}{3,6}\;\frac{\mathrm m}{\mathrm s}=5\;\mathrm{m/s} \end{gather} \]
El desplazamiento total del trabajador en bicicleta, ΔS, será la suma de los desplazamientos a pie, ΔS1, y en autobús, ΔS2
\[ \begin{gather} \Delta S=\Delta S_1+\Delta S_2 \tag{I} \end{gather} \]
el desplazamiento a pie ya se da en el problema como ΔS1 = 500 m. Como el autobús se desplaza a velocidad constante, su velocidad coincide con la velocidad media, utilizando la expresión de velocidad media
\[ \begin{gather} \bbox[#99CCFF,10px] {v_m=\frac{\Delta S}{\Delta t}} \end{gather} \]
\[ \begin{gather} v_2=\frac{\Delta S_2}{\Delta t_2}\\[5pt] \Delta S_2=v_2\;\Delta t_2\\[5pt] \Delta S_2=5\times2400\\[5pt] \Delta S_2=12000\;\mathrm m \end{gather} \]
De la expresión (I), el desplazamiento total será
\[ \begin{gather} \Delta S=600+12000\\[5pt] \Delta S=12600\;\mathrm m \end{gather} \]
Como la velocidad de la bicicleta es constante, también usamos la expresión de velocidad media para conocer el tiempo total del trayecto Δt
\[ \begin{gather} v_3=\frac{\Delta S}{\Delta t}\\[5pt] \Delta t=\frac{\Delta S}{v_3}\\[5pt] \Delta t=\frac{12600}{6}\\[5pt] \Delta t=2100\;\mathrm s \end{gather} \]
convirtiendo este valor a minutos
\[ \begin{gather} \Delta t=2100\;\cancel{\mathrm s}\times\frac{1\;\mathrm{min}}{60\;\cancel{\mathrm s}}=35\;\mathrm{min} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta t=35\;\mathrm{min}} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .