Exercice Résolu sur les Mouvement Unidimensionnel
publicité   



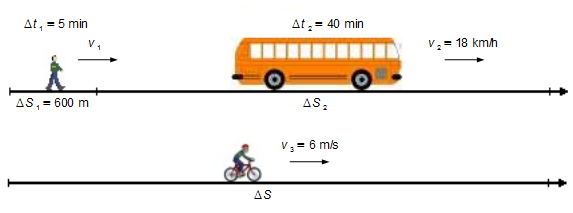
Un ouvrier sort de chez lui et marche pendant 600 mètres en 5 minutes jusqu'à l'arrêt de bus. Une fois arrivé à l'arrêt, il prend le bus et voyage pendant 40 minutes à une vitesse constante de 18 kilomètres par heure jusqu'à l'usine où il travaille. Si jamais il faisait tout le trajet à vélo, à une vitesse constante de 6 mètres par seconde. Combien de temps mettrait-il de chez lui à l'usine ? Donnez la réponse en minutes.


Données du problème:
  • Distance de chez lui à l'arrêt de bus:    ΔS1 = 600 m;
  • Intervalle de temps de chez lui à l'arrêt de bus:    Δt1 = 5 min;
  • Intervalle de temps de l'arrêt de bus à l'usine:    Δt2 = 40 min;
  • Vitesse du bus:    vo = 18 km/h;
  • Vitesse du vélo:    v3 = 6 m/s.
Schéma du problème:

Nous choisissons un référentiel orienté vers la droite (Figure 1)

Figura 1

Solution

Convertissant les intervalles de temps donnés en minutes en secondes et la vitesse du bus donnée en kilomètres par heure en mètres par seconde utilisés dans le Système International d'Unités (SI)
\[ \begin{gather} \Delta t_1=5\;\cancel{\mathrm{min}}\times\frac{60\;\mathrm s}{1\;\cancel{\mathrm{min}}}=300\;\mathrm s\\[10pt] \Delta t_2=40\;\cancel{\mathrm{min}}\times\frac{60\;\mathrm s}{1\;\cancel{\mathrm{min}}}=2400\;\mathrm s\\[10pt] v_2=18\;\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{18}{3,6}\;\frac{\mathrm m}{\mathrm s}=5\;\mathrm{m/s} \end{gather} \]
Le déplacement total de l'ouvrier à vélo, ΔS, sera la somme des déplacements à pied, ΔS1, et en bus, ΔS2
\[ \begin{gather} \Delta S=\Delta S_1+\Delta S_2 \tag{I} \end{gather} \]
le déplacement à pied est déjà donné dans le problème ΔS1 = 500 m, puisque le bus se déplace à vitesse constante, sa vitesse correspond à la vitesse moyenne, en utilisant l'expression de la vitesse moyenne
\[ \begin{gather} \bbox[#99CCFF,10px] {v_m=\frac{\Delta S}{\Delta t}} \end{gather} \]
\[ \begin{gather} v_2=\frac{\Delta S_2}{\Delta t_2}\\[5pt] \Delta S_2=v_2\;\Delta t_2\\[5pt] \Delta S_2=5\times2400\\[5pt] \Delta S_2=12000\;\mathrm m \end{gather} \]
De l'expression (I), le déplacement total sera
\[ \begin{gather} \Delta S=600+12000\\[5pt] \Delta S=12600\;\mathrm m \end{gather} \]
comme la vitesse du vélo est également constante, nous utilisons également l'expression de la vitesse moyenne pour connaître le temps total du trajet Δt
\[ \begin{gather} v_3=\frac{\Delta S}{\Delta t}\\[5pt] \Delta t=\frac{\Delta S}{v_3}\\[5pt] \Delta t=\frac{12600}{6}\\[5pt] \Delta t=2100\;\mathrm s \end{gather} \]
en convertissant cette valeur en minutes
\[ \begin{gather} \Delta t=2100\;\cancel{\mathrm s}\times\frac{1\;\mathrm{min}}{60\;\cancel{\mathrm s}}=35\;\mathrm{min} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta t=35\;\mathrm{min}} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .