Solved Problem on One-dimensional Motion
advertisement
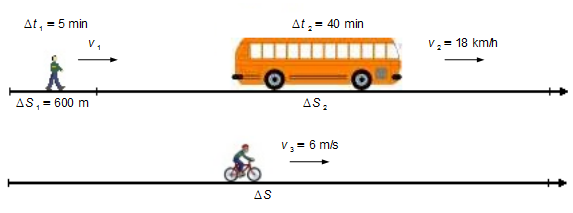
A worker leaves his house and walks for 600 meters in 5 minutes to the bus stop, as soon as he reaches the bus stop he takes the bus and travels for 40 minutes at a constant speed of 18 kilometers per hour to the factory where he works. If he took the entire route by bike, at a constant speed of 6 meters per second. How long would it take from home to the factory? Answer in minutes.
Problem data:
- Distance from the house to the bus stop: ΔS1 = 600 m;
- Time interval from house to bus stop: Δt1} = 5 min;
- Time interval from the bus stop to the factory: Δt2 = 40 min;
- Speed of the bus: vo = 18 km/h;
- Speed of the bicycle: v3 = 6 m/s.
We choose a frame of reference oriented to the right (Figure 1)
Solution
Converting the given time intervals in minutes to seconds and the bus speed given in kilometers per hour to meters per second used in the International System of Units (SI)
\[
\begin{gather}
\Delta t_1=5\;\cancel{\mathrm{min}}\times\frac{60\;\mathrm s}{1\;\cancel{\mathrm{min}}}=300\;\mathrm s\\[10pt]
\Delta t_2=40\;\cancel{\mathrm{min}}\times\frac{60\;\mathrm s}{1\;\cancel{\mathrm{min}}}=2400\;\mathrm s\\[10pt]
v_2=18\;\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{18}{3,6}\;\frac{\mathrm m}{\mathrm s}=5\;\mathrm{m/s}
\end{gather}
\]
The total displacement of the worker by bicycle, ΔS, will be the sum of the displacements by
foot, ΔS1, and bus, ΔS2
\[
\begin{gather}
\Delta S=\Delta S_1+\Delta S_2 \tag{I}
\end{gather}
\]
the foot displacement is already given in the problem ΔS1 = 500 m, as the bus moves
with onstant speed, its speed coincides with the average speed, using the expression the average speed
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\bar v=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
\[
\begin{gather}
v_2=\frac{\Delta S_2}{\Delta t_2}\\[5pt]
\Delta S_2=v_2\;\Delta t_2\\[5pt]
\Delta S_2=\left(5\;\mathrm{\small{\frac{m}{\cancel s}}}\right)\left(2400\;\mathrm{\cancel s}\right)\\[5pt]
\Delta S_2=12000\;\mathrm m
\end{gather}
\]
From expression (I), the total displacement will be
\[
\begin{gather}
\Delta S=600\;\mathrm m+12000\;\mathrm m\\[5pt]
\Delta S=12600\;\;\mathrm m
\end{gather}
\]
as the speed of the bicycle is constant, we use the expression of the average speed to know the total time of
the route Δt
\[
\begin{gather}
v_3=\frac{\Delta S}{\Delta t}\\[5pt]
\Delta t=\frac{\Delta S}{v_3}\\[5pt]
\Delta t=\frac{12600\;\mathrm{\cancel m}}{6\;\mathrm{\frac{\cancel m}{s}}}\\[5pt]
\Delta t=2100\;\text{s}
\end{gather}
\]
converting this value to minutes
\[
\begin{gather}
\Delta t=2100\;\cancel{\mathrm s}\times\frac{1\;\mathrm{min}}{60\;\cancel{\mathrm s}}=35\;\mathrm{min}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta t=35\;\mathrm{min}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .