Ejercicio Resuelto sobre Trabajo y Energía
publicidad
Un objeto con peso de 10 N es levantado, desde el reposo, por una fuerza de 30 N hasta una altura de 5 m. Determine:
a) El trabajo de la fuerza aplicada para levantar el objeto hasta la altura dada;
b) El trabajo del peso;
c) La velocidad del cuerpo al alcanzar la altura dada.
Datos del problema:
- Peso del cuerpo: P = 10 N;
- Fuerza aplicada al cuerpo: F = 30 N;
- Altura a la que se levanta el cuerpo: h = 5 m;
- Velocidad inicial del cuerpo: v0 = 0;
- Aceleración de la gravedad: g = 9,8 m/s2.
Adoptamos un sistema de referencia con origen en el suelo y orientado hacia arriba, en este caso la
aceleración de la gravedad y el peso del cuerpo serán negativos (Figura 1).
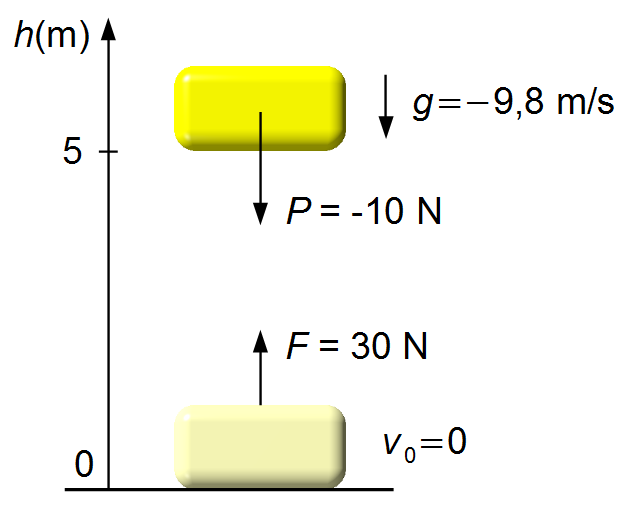
Solución
a) El trabajo de una fuerza es da por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{W_{\small F}=Fd} \tag{I}
\end{gather}
\]
en este caso la fuerza es la fuerza externa, F, que levanta el peso, y la distancia será la altura,
h, a la que el peso fue elevado
\[
\begin{gather}
W_{\small F}=Fh\\[5pt]
W_{\small F}=30\times 5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{W_{\small F}=150\;\mathrm J}
\end{gather}
\]
b) Aplicando la ecuación (I) para el peso
\[
\begin{gather}
W_{\small P}=Ph\\[5pt]
W_{\small P}=-10\times 5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{W_{\small P}=-50\;\mathrm J}
\end{gather}
\]
Observación: no existe energía negativa, el signo negativo indica que el trabajo se realizó
en la dirección opuesta a orientación del campo gravitacional. El campo gravitacional apunta hacia la
Tierra y el objeto se alejó al ser elevado.
c) La fuerza resultante, FR, entre la fuerza externa y la fuerza peso es igual a
\[
\begin{gather}
F_{\small R}=F-P\\[5pt]
F_{\small R}=30-10\\[5pt]
F_{\small R}=20\;\mathrm N
\end{gather}
\]
el peso es dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg}
\end{gather}
\]
\[
\begin{gather}
m=\frac{P}{g}\\[5pt]
m=\frac{-10}{-9,8}\\[5pt]
m\approx1\;\mathrm{kg}
\end{gather}
\]
Por el Teorema del Trabajo y la Energía, el Trabajo de una fuerza es igual a la variación de la
Energía Cinética
\[
\begin{gather}
\bbox[#99CCFF,10px]
{W_{\small F}=\Delta E_c=E_{c f}-E_{c i}} \tag{II}
\end{gather}
\]
la energía cinética es dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_c=\frac{mv^2}{2}} \tag{III}
\end{gather}
\]
sustituyendo las ecuaciones (I) y (III) en la ecuación (II), el trabajo de la fuerza resultante para elevar
el cuerpo es dado por
\[
\begin{gather}
F_{\small R}h=\frac{mv^2}{2}-\frac{mv_0^2}{2}\\[5pt]
v=\sqrt{\frac{2}{m}\left[F_{\small R}h+\frac{mv_0^2}{2}\right]\;}\\[5pt]
v=\sqrt{\frac{2}{1}\left[20\times 5+\frac{1\times 0^2}{2}\right]\;}\\[5pt]
v=\sqrt{\frac{2}{1}\times\left[100\right]\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v\approx 14.1\;\mathrm{m/s}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .