Ejercicio Resuelto sobre Dinámica
publicidad   



Dos bloques, con masas de 3 kg y 2 kg, parten del reposo en lo alto de un plano inclinado de 30° y recorren una distancia de 40 m hasta la base del plano. No hay fricción entre los bloques y el plano inclinado. Determine cuál de los bloques llegará al final con la mayor velocidad.


Datos del problema:
  • Masa del bloque A:    mA = 3 kg;
  • Masa del bloque B:    mB = 2 kg;
  • Velocidad inicial del bloque A:    v0A = 0;
  • Velocidad inicial del bloque B:    v0B = 0;
  • Longitud del plano inclinado:    L = 40 m;
  • Ángulo de inclinación del plano:    θ = 30°;
  • Aceleración de la gravedad:    g = 9,8 m/s2.
Esquema del problema:

Tomando un sistema de referencia orientado en la dirección descendente del plano inclinado y con el eje-x paralelo al plano (Figura 1).

Figura 1

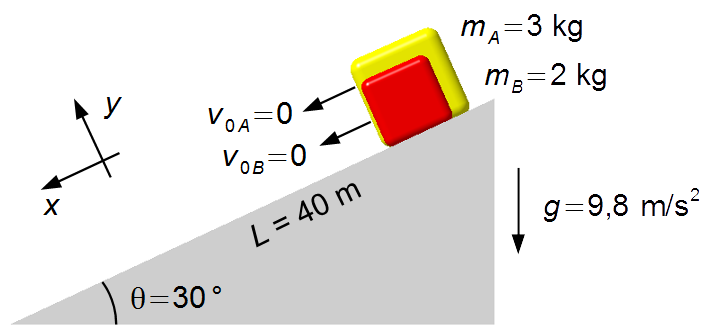
Haciendo un Diagrama de Cuerpo Libre tenemos las fuerzas que actúan sobre los bloques.

  • Bloque A (Figura 2-A):
    • \( {\vec P}_{\small A} \): peso del bloque A;
    • \( {\vec N}_{\small A} \): fuerza de reacción normal de la superficie sobre el bloque A.
El peso puede descomponerse en dos, una componente paralela al eje-x, \( {\vec P}_{\small AP} \), y la otra perpendicular, \( {\vec P}_{\small AN} \) (Figura 2-A).
Dibujamos las fuerzas en un sistema de ejes xy (Figura 2-B)
Figura 2

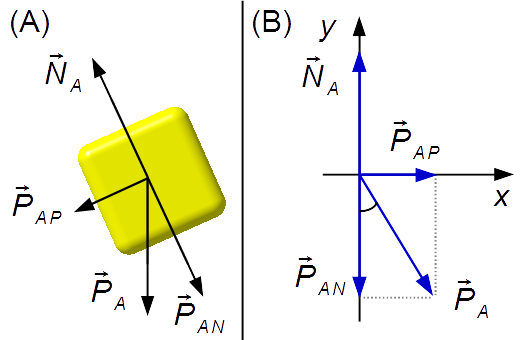
  • Bloque B (Figura 3-A):
    • \( {\vec P}_{\small B} \): peso del bloque B;
    • \( {\vec N}_{\small B} \): fuerza de reacción normal de la superficie sobre el bloque B.
El peso puede descomponerse en dos, una componente paralela al eje-x, \( {\vec P}_{\small BP} \), y la otra perpendicular, \( {\vec P}_{\small BN} \) (Figura 3-A).
Dibujamos las fuerzas en un sistema de ejes xy (Figura 3-B)
Figura 3

Solución

Aplicando la Segunda Ley de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Bloque A:
    • Dirección x:
\[ \begin{gather} P_{\small AP}=m_{\small A}a_{\small A} \tag{I} \end{gather} \]
la componente paralela del peso es dada por
\[ \begin{gather} P_{\small AP}=P_{\small A}\operatorname{sen}\theta \tag{II} \end{gather} \]
sustituyendo la ecuación (II) en la ecuación (I)
\[ \begin{gather} P_{\small A}\operatorname{sen}\theta=m_{\small A}a_{\small A} \tag{III} \end{gather} \]
el peso es dado por
\[ \begin {gather} \bbox[#99CCFF,10px] {P=mg} \tag{IV} \end{gather} \]
para el bloque A
\[ \begin{gather} P_{\small A}=m_{\small A}g \tag{V} \end{gather} \]
sustituyendo la ecuación (V) en la ecuación (III)
\[ \begin{gather} \cancel{m_{\small A}}g\operatorname{sen}\theta =\cancel{m_{\small A}}a_{\small A}\\[5pt] a_{\small A}=g\operatorname{sen}30° \end{gather} \]

De la Trigonometría tenemos que   \( \operatorname{sen}30°=\dfrac{1}{2} \)

\[ \begin{gather} a_{\small A}=9,8\times\frac{1}{2}\\[5pt] a_{\small A}=4,9\;\mathrm{m/s^2} \tag{VI} \end{gather} \]
  • Bloque B:
    • Dirección x:
\[ \begin{gather} P_{\small BP}=m_{\small B}a_{\small B} \tag{VII} \end{gather} \]
la componente paralela del peso es dada por
\[ \begin{gather} P_{\small BP}=P_{\small B}\operatorname{sen}\theta \tag{VIII} \end{gather} \]
sustituyendo la ecuación (VIII) en la ecuación (VII)
\[ \begin{gather} P_{\small B}\operatorname{sen}\theta=m_{\small B}a_{\small B} \tag{IX} \end{gather} \]
para el bloque B usando la ecuación (IV) para el peso
\[ \begin{gather} P_{\small B}=m_{\small B}g \tag{X} \end{gather} \]
sustituyendo la ecuación (X) en la ecuación (IX)
\[ \begin{gather} \cancel{m_{\small B}}g\operatorname{sen}\theta =\cancel{m_{\small B}}a_{\small B}\\[5pt] a_{\small B}=g\operatorname{sen}30°\\[5pt] a_{\small B}=9,8\times\frac{1}{2}\\[5pt] a_{\small B}=4,9\;\mathrm{m/s^2} \tag{XII} \end{gather} \]
Comparando las expresiones (VI) y (XII) vemos que los dos bloques tienen la misma aceleración, y como ambos parten con la misma velocidad y recorren la misma distancia (40 m), podemos concluir que ambos llegan con la misma velocidad al final de la trayectoria.

Observación: Calculando la velocidad final.
Aplicando la ecuación de la velocidad en función del desplazamiento
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
Los dos bloques tienen la misma aceleración (aA = aB = a = 5 m/s2), la misma velocidad inicial (v0A = v0B = v0 = 0) y recorren la misma distancia (L = 40 m), la velocidad final será
\[ \begin{gather} v^2=0^2+2\times 5\times 40\\[5pt] v=\sqrt{400\;}\\[5pt] v=20\;\mathrm{m/s} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .