Exercice Résolu sur les Dynamique
publicité   



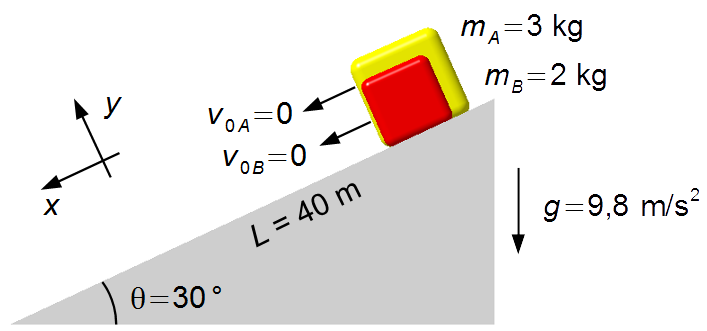
Deux blocs, de masses 3 kg et 2 kg, sont abandonnés depuis le repos en haut d'un plan incliné de 30° et parcourent une distance de 40 m jusqu'à la base du plan. Il n'y a pas de frottement entre les blocs et le plan incliné. Déterminer lequel des blocs arrivera à la fin avec la plus grande vitesse.


Données du problème:
  • Masse du bloc A:    mA = 3 kg;
  • Masse du bloc B:    mB = 2 kg;
  • Vitesse initiale du bloc A:    v0A = 0;
  • Vitesse initiale du bloc B:    v0B = 0;
  • Longueur du plan incliné:    L = 40 m;
  • Angle d'inclinaison du plan:    θ = 30°;
  • Accélération de la pesanteur:    g = 9,8 m/s2.
Schéma du problème:

Nous choisissons un référentiel dirigé vers le bas du plan incliné et avec l'axe-x parallèle au plan (Figure 1).

Figure 1

En faisant un Diagramme de Corps Libre, nous avons les forces agissant sur les blocs.

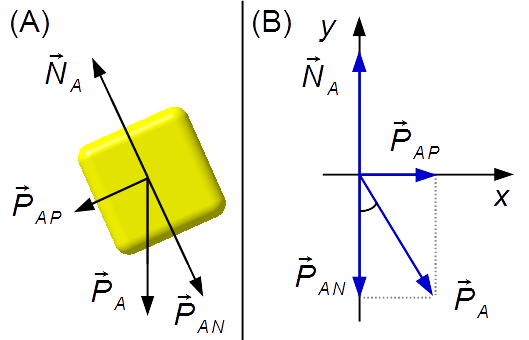
  • Bloc A (Figure 2-A):
    • \( {\vec P}_{\small A} \): poids du bloc A;
    • \( {\vec N}_{\small A} \): force de réaction normale de la surface sur le bloc A.
Le poids peut être décomposée en deux, une composante parallèle à l'axe-x, \( {\vec P}_{\small AP} \), et l'autre perpendiculaire, \( {\vec P}_{\small AN} \) (Figure 2-A).
Nous dessinons les forces dans un système de coordonnées Oxy (Figure 2-B)
Figure 2

  • Bloc B (Figure 3-A):
    • \( {\vec P}_{\small B} \): poids du bloc B;
    • \( {\vec N}_{\small B} \): force de réaction normale de la surface sur le bloc B.
Le poids peut être décomposée en deux, une composante parallèle à l'axe x, \( {\vec P}_{\small BP} \), et l'autre normale ou perpendiculaire, \( {\vec P}_{\small BN} \) (Figure 3-A).
Nous dessinons les forces dans un système de coordonnées Oxy (Figure 3-B)
Figure 3

Solution

En appliquant la Deuxième Loi de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Bloc A:
    • Direction x:
\[ \begin{gather} P_{\small AP}=m_{\small A}a_{\small A} \tag{I} \end{gather} \]
la composante parallèle du poids est donnée par
\[ \begin{gather} P_{\small AP}=P_{\small A}\sin \theta \tag{II} \end{gather} \]
en substituant l'équation (II) dans l'équation (I)
\[ \begin{gather} P_{\small A}\sin \theta=m_{\small A}a_{\small A} \tag{III} \end{gather} \]
le poids est donnée par
\[ \begin {gather} \bbox[#99CCFF,10px] {P=mg} \tag{IV} \end{gather} \]
pour le bloc A
\[ \begin{gather} P_{\small A}=m_{\small A}g \tag{V} \end{gather} \]
en substituant l'équation (V) dans l'équation (III)
\[ \begin{gather} \cancel{m_{\small A}}g\sin \theta =\cancel{m_{\small A}}a_{\small A}\\[5pt] a_{\small A}=g\sin 30° \end{gather} \]

En Trigonométrie, nous avons   \( \sin 30°=\dfrac{1}{2} \)

\[ \begin{gather} a_{\small A}=9,8\times\frac{1}{2}\\[5pt] a_{\small A}=4,9\;\mathrm{m/s^2} \tag{VI} \end{gather} \]
  • Bloc B:
    • Direction x:
\[ \begin{gather} P_{\small BP}=m_{\small B}a_{\small B} \tag{VII} \end{gather} \]
La composante parallèle du poids est donnée par
\[ \begin{gather} P_{\small BP}=P_{\small B}\sin \theta \tag{VIII} \end{gather} \]
en substituant l'équation (VIII) dans l'équation (VII)
\[ \begin{gather} P_{\small B}\sin \theta=m_{\small B}a_{\small B} \tag{IX} \end{gather} \]
pour le bloc B en utilisant l'équation (IV) pour le poids
\[ \begin{gather} P_{\small B}=m_{\small B}g \tag{X} \end{gather} \]
en substituant l'équation (X) dans l'équation (IX)
\[ \begin{gather} \cancel{m_{\small B}}g\sin \theta =\cancel{m_{\small B}}a_{\small B}\\[5pt] a_{\small B}=g\sin 30°\\[5pt] a_{\small B}=9,8\times\frac{1}{2}\\[5pt] a_{\small B}=4,9\;\mathrm{m/s^2} \tag{XII} \end{gather} \]
En comparant les expressions (VI) et (XII), nous voyons que les deux blocs ont la même accélération, et comme ils partent tous deux avec la même vitesse et parcourent la même distance (40 m), nous pouvons conclure que les deux arrivent avec la même vitesse à la fin de la trajectoire.

Remarque: Calcul de la vitesse finale.
En appliquant l'équation de la vitesse en fonction de l'accélération et du déplacement
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
Les deux blocs ont la même accélération (aA = aB = a = 5 m/s2), la même vitesse initiale (v0A = v0B = v0 = 0) et parcourent la même distance (L = 40 m), la vitesse finale sera
\[ \begin{gather} v^2=0^2+2\times 5\times 40\\[5pt] v=\sqrt{400\;}\\[5pt] v=20\;\mathrm{m/s} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .