Ejercicio Resuelto sobre Impulso
publicidad   



Desde la cima de un edificio de 100 m de altura se deja caer, desde el reposo, un ladrillo de masa 900 g bajo la acción del peso. Calcular:
a) La velocidad del ladrillo al tocar el suelo;
b) La cantidad de movimiento del ladrillo al tocar el suelo;
c) El impulso de la fuerza actuante sobre el ladrillo durante la caída.


Datos del problema:
  • Altura de la caída:    S = 100 m;
  • Masa del ladrillo:    m = 900 g;
  • Velocidad inicial del ladrillo:    v0 = 0;
  • Aceleración de la gravedad:    g = 9,8 m/s2.
Esquema del problema:

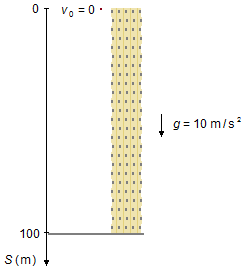
Tomaamos un sistema de referencia orientado hacia abajo con origen en la cima del edificio. Como el ladrillo parte del reposo, su velocidad inicial es nula, v0 = 0, su posición inicial también es nula, S0 = 0, y la aceleración de la gravedad está en el mismo sentido del sistema de referencia (Figura 1).
Figura 1

Solución

Primero, debemos convertir la masa del ladrillo dada en gramos (g) a kilogramos (kg), utilizado en el Sistema Internacional de Unidades (SI)
\[ \begin{gather} m=900\;\mathrm{\cancel g}\times\frac{1\;\mathrm{kg}}{1000\;\mathrm{\cancel g}}=0,9\;\mathrm{kg} \end{gather} \]
a) El ladrillo cae en caída libre bajo la acción de la aceleración de la gravedad, utilizando la ecuación de la velocidad en función del desplazamiento
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
la aceleración del movimiento es la misma aceleración de la gravedad, a = g, y sustituyendo los valores
\[ \begin{gather} v^2=v_0^2+2g(S-S_{0})\\[5pt] v^2=0^2+2\times 9,8\times(100-0)\\[5pt] v^2=0+1960\\[5pt] v=\sqrt{1960\;} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {v\simeq 44,3\;\mathrm{m/s}} \end{gather} \]

b) La cantidad de movimiento está dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {p=mv} \tag{I} \end{gather} \]
sustituyendo la masa dada para el ladrillo y la velocidad calculada en el item anterior
\[ \begin{gather} p=0,9\times 44,3 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {p=39,9\;\mathrm{kg.m/s}} \end{gather} \]

c) Por el Teorema del Impulso
\[ \begin{gather} \bbox[#99CCFF,10px] {I=\Delta p=p_{f}-p_{i}} \end{gather} \]
sustituyendo la expresión (I) para las cantidades de movimiento inicial y final del ladrillo
\[ \begin{gather} I=mv_{f}-mv_{i} \end{gather} \]
siendo la velocidad final, vf = v, calculada en el apartado (a), y la velocidad inicial, vi = v0 = 0
\[ \begin{gather} I=mv-mv_{0}\\[5pt] I=0,9\times 44,3-0,9\times 0\\[5pt] I=40,2-0 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {I=39,9\;\mathrm{N.s}} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .