Solved Problem on Dynamics
ES
FR
PT-BR
advertisement
A man of mass m = 70 kg, is in an elevator, this one moves with acceleration a = 2 m/s2. Determine:
a) The force of the man on the floor of the elevator, if the elevator is accelerating downwards;
b) The force of the man on the floor of the elevator, if the elevator is accelerating upwards;
c) For what acceleration of the elevator will the force of the man on the floor will be equal to zero?
Problem data:
- Mass of the man: m = 70 kg;
- Acceleration of the elevator: a = 2 m/s2;
- Acceleration due to gravity: g = 9.8 m/s2.
a) We choose the acceleration in the direction in which the elevator moves downward as positive.
Drawing a Free-Body Diagram for the elevator and the man (Figure 1).
-
Elevator:
- \( \vec N \): action of the man on the floor of the elevator.
-
Mam:
- \( \vec W \): weight of the man;
- \( \vec N \): normal reaction force of the elevator on the man.
Note: in the elevator, there is also the weight of the elevator itself, but as we want
to find the force that man makes on the elevator and this is equal, in magnitude, to the normal of
the elevator on the man,
\( \vec N \),
it is sufficient to analyze the forces acting on the man.
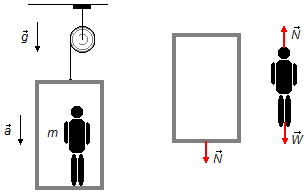
Applying Newton's Second Law
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a}
\end{gather}
\]
- Man:
\[
\begin{gather}
W-N=ma \tag{I}
\end{gather}
\]
the weight is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{W=mg}
\end{gather}
\]
substituting this equation into equation (I)
\[
\begin{gather}
mg-N=ma\\[5pt]
N=m\;(g-a) \tag{II}\\[5pt]
N=\left(70\;\mathrm{kg}\right)\left(9.8\;\mathrm{m/s^2}-2\;\mathrm{m/s^2}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{N=560\;\mathrm N}
\end{gather}
\]
b) We choose the acceleration in the direction in which the elevator moves upward as positive.
Once again, drawing a Free Body Diagram, we have the forces that act on the bodies (Figure 2), and we can apply Newton's Second Law.
The forces acting on the elevator and the man are the same as in item (a), (Figures 1 and 2).
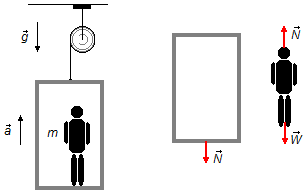
Using the equation (I) for the man, with the inversion in the direction of the acceleration of the elevator
\[
\begin{gather}
N-mg=ma\\[5pt]
N=m\;(g+a) \tag{III}\\[5pt]
N=\left(70\;\mathrm{kg}\right)\left(9.8\;\mathrm{m/s^2}+2\;\mathrm{m/s^2}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{N=825\;\mathrm N}
\end{gather}
\]
c) If the man does not exert force on the floor of the elevator we have the normal force null, N = 0, substituting this condition in the equation (II) of item (a)
\[
\begin{gather}
0=m\;(g-a)\\[5pt]
g-a=\frac{0}{m}\\[5pt]
g-a=0
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a=g=9.8\;\mathrm{m/s^2}}
\end{gather}
\]
Note 1: this result means that the elevator and the man are in free fall, the man tends to
"take off" from the elevator floor, and there is no action of the man on the elevator, therefore there
is no reaction force on the man due to the elevator.
Note 2: if instead of using the equation (II) of item (a), we had used the equation (III) of item (b), with the condition of N = 0, the result would be a = −g. This means that the magnitude of the acceleration would be the same, but the direction of acceleration, which in item (b) is pointed upwards, would have to be downwards, which would coincide with the situation of item (a).
Note 2: if instead of using the equation (II) of item (a), we had used the equation (III) of item (b), with the condition of N = 0, the result would be a = −g. This means that the magnitude of the acceleration would be the same, but the direction of acceleration, which in item (b) is pointed upwards, would have to be downwards, which would coincide with the situation of item (a).
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .