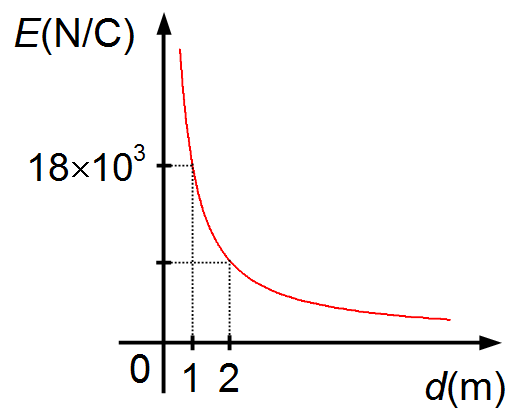
Gelöste Übung zu Elektrisches Feld
Werbung   

Die Grafik stellt die Änderung des elektrischen Feldes dar, das von einer positiven Punktladung Q in als Funktion vom Abstand zur Ladung erzeugt wird. Die Coulomb-Konstante im Vakuum ist \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \). Bestimmen Sie:
a) Den Wert der Ladung Q;
b) Die Stärke der elektrischen Kraft, die auf eine Ladung q = −1×10−5 C wirkt, die sich in 2 m Entfernung von Q befindet;
c) Die Stärke der elektrischen Kraft, die auf eine Ladung q = 1×10−5 C wirkt, die sich in 1 m Entfernung von Q befindet.

 

Gegebene Daten:

  • Elektrische Ladung in Situation 1:    q1 = −1×10−5 C;
  • Abstand zwischen der Ladung Q umd q1:    d1 = 2 m;
  • Elektrische Ladung in Situation 2:    q2 = 1×10−5 C;
  • Abstand zwischen der Ladung Q und q2:    d2 = 1 m;
  • Coulomb-Konstante im Vakuum:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

Lösung:

a) Die Stärke des elektrischen Feldes wird durch

\[ \begin{gather} \bbox[#99CCFF,10px] {E=k_0\frac{q}{r^2}} \end{gather} \]

Aus der Grafik entnehmen wir, dass bei einem Abstand r = 1 m von der Ladung Q das elektrische Feld den Wert E = 18×103 N/C hat. Wenn wir diese Werte einsetzen, erhalten wir den Wert der Ladung Q

\[ \begin{gather} E=k_0\frac{Q}{r^2} \\[5pt] Q=\frac{Er^2}{k_0} \\[5pt] Q=\frac{18\times 10^3\times 1^2}{9\times 10^9} \\[5pt] Q=2\times 10^3\times 10^{-9} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=2\times 10^{-6}\;\mathrm C} \end{gather} \]

 

b) Nach dem Coulomb-Gesetz wird die Stärke der elektrischen Kraft durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_0\frac{|\;q_1\;||\;q_2\;|}{r^2}} \tag{I} \end{gather} \]

einsetzen des im Teil (a) gefundenen Ladungswertes und r = d1

\[ \begin{gather} F_{\small E}=k_0\frac{|\;Q\;||\;q_1\;|}{d_1^2} \\[5pt] F_{\small E}=9\times 10^9\times\frac{2\times 10^{-6}\times 1\times 10^{-5}}{2^2} \\[5pt] F_{\small E}=4,5\times10^9\times 10^{-11} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{\small E}=4,5\times 10^{-2}\;\mathrm N} \end{gather} \]

 

c) Erneutes Anwenden der Gleichung (I) und Einsetzen des im Teil (a) bestimmten Ladungswertes sowie r = d2

\[ \begin{gather} F_{\small E}=k_0\frac{|\;Q\;||\;q_2\;|}{d_2^2} \\[5pt] F_{\small E}=9\times 10^9\times\frac{2\times 10^{-6}\times 1\times 10^{-5}}{1^2} \\[5pt] F_{\small E}=18\times 10^9\times 10^{-11} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{\small E}=18\times 10^{-2}\;\mathrm N} \end{gather} \]
Anmerkung: Die Ladung 1 ist negativ, die auf sie wirkende Kraft hat dieselbe Richtung, aber die entgegengesetzte Orientierung zum elektrischen Feld, also in Richtung der Ladung Q – entgegengesetzte Ladungen ziehen sich an. Die Ladung 2 ist positiv. Die auf sie wirkende Kraft hat dieselbe Richtung und Orientierung wie das elektrische Feld, also in entgegengesetzte Richtung zur Ladung Q – gleichnamige Ladungen stoßen sich ab.
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .