Exercice Résolu sur les Force Électrique
publicité
Deux charges de même module et de signes opposés sont fixées sur une ligne horizontale à une distance d l'une de l'autre. Une sphère de masse m chargée avec une charge électrique, est suspendue à un fil et est d'abord approchée de l'une des charges jusqu'à ce qu'elle soit en équilibre exactement au-dessus de celle-ci à une hauteur d. Ensuite, le fil est déplacé en direction de la deuxième charge jusqu'à ce que la sphère soit en équilibre au-dessus de la deuxième charge. Trouvez les angles de déviation du fil dans les deux situations, en sachant que l'angle de déviation au-dessus de la première charge est deux fois plus grand que l'angle de déviation au-dessus de la deuxième charge.
Données du problème:
- Distance entre les charges sur l'horizontale: d;
- Distance entre les charges sur la verticale: d;
- Masse de la sphère: m;
- Relation entre les angles de déviation: θ1 = 2θ2.
Nous choisissons que les charges fixes, 1 et 2 dans la Figure 1, aient une valeur de −Q et +Q, et que la charge suspendue au fil ait une charge de +q (charge 3).
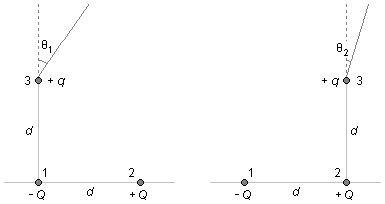
Dans les situations d'équilibre, il y a une distance d entre les charges fixes sur l'horizontale, et la charge suspendue se trouve à une distance d sur la verticale. L'angle θ1 est le double de θ2, selon les données du problème.
Solution:
Initialement, la charge +q est approchée de la première charge −Q sur la verticale. Sur la charge +q, agissent le poids P, la force de tension T1, la force électrique d'attraction entre +q et −Q, F31, et la force électrique de répulsion entre +q et +Q, F32 (Figure 2-A). Les forces sur la verticale s'équilibrent, ne restant que la composante horizontale de la force de répulsion F32 qui déplace la charge +q de sa position d'équilibre. Pour rétablir l'équilibre, elle doit être déplacée vers la droite (Figure 2-B) jusqu'à être à la verticale de la charge −Q. À ce moment, le fil qui maintient la charge +q forme un angle θ1 avec la verticale (Figure 2-C).
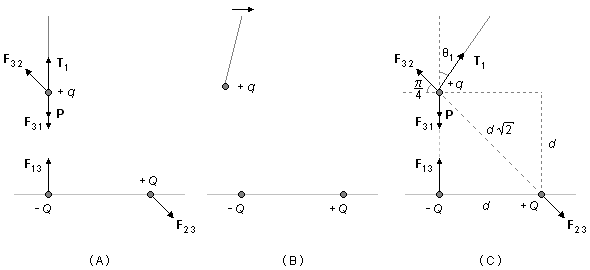
La force entre les charges +q et −Q, F31, agit le long du côté du carré qui mesure d. Selon la Loi de Coulomb, le module de cette force sera
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{el}=\frac{1}{4\pi\varepsilon_0}\frac{|q_{A}||q_{B}|}{r^2}}
\end{gather}
\]
\[
\begin{gather}
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_1|}{r^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q||-Q|}{d^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2} \tag{I}
\end{gather}
\]
La force entre les charges +q et +Q, F32, agit le long de la diagonale d'un
carré de côté d, formé par la distance entre les charges +Q et −Q et par la
hauteur de la charge +q. La diagonale vaut
\( d\sqrt{2\;} \),
et cette force forme un angle
\( \frac{\pi}{4} \)
avec l'horizontale, et le module sera
\[
\begin{gather}
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_2|}{r^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q||Q|}{\left(d\sqrt{2\;}\right)^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2} \tag{II}
\end{gather}
\]
Comme la sphère est en équilibre, la somme des forces qui agissent sur elle est nulle
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum \mathbf F=0}
\end{gather}
\]
en appliquant cette condition à la situation 1 (Figure 3)
\[
\begin{gather}
\mathbf F_{32}+\mathbf T_1+\mathbf F_{31}+\mathbf P=0
\end{gather}
\]
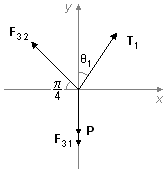
où
\( \mathbf F_{32}=-F_{32}\cos\dfrac{\pi}{4}\;\mathbf i+F_{32}\sin\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf T_1=T_1\sin\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
en substituant les valeurs de (I) et (II)
\[
\begin{gather}
-F_{32}\cos\frac{\pi}{4}\;\mathbf i+F_{32}\sin\frac{\pi}{4}\;\mathbf j+T_1\sin\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j-F_{31}\;\mathbf j-mg\;\mathbf j=0\\[5pt]
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}\;\mathbf i+\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf j+T_1\sin\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\;\mathbf j-mg\;\mathbf j=0
\end{gather}
\]
en séparant les composantes
- Direction i:
\[
\begin{gather}
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}+T_1\sin\theta_1=0\\[5pt]
T_1\sin\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4} \tag{III}
\end{gather}
\]
- Direction j:
\[
\begin{gather}
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}+T_1\cos\theta_1-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}-mg=0\\[5pt]
T_1\cos\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4}+mg\\[5pt]
T_1\cos\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\left(1-\frac{\sqrt{2\;}}{4}\right)+mg \tag{IV}
\end{gather}
\]
De la même manière, dans le second cas, la charge +q est approchée de la deuxième charge +Q sur
la verticale. Sur la charge +q, agissent le poids P, la force de tension du fil,
T2, la force d'attraction entre +q et −Q, F31, et la
force de répulsion entre +q et +Q, F32 (Figure 4-A). Les forces sur la
verticale s'équilibrent, ne restant que la composante horizontale de la force d'attraction
F31 qui déplace la charge +q de sa position d'équilibre. Pour rétablir l'équilibre,
elle doit être déplacée vers la droite (Figure 4-B) jusqu'à être à la verticale de la charge −Q.
À ce moment, le fil qui maintient la charge +q forme un angle θ2 avec la
verticale (Figure 4-C).
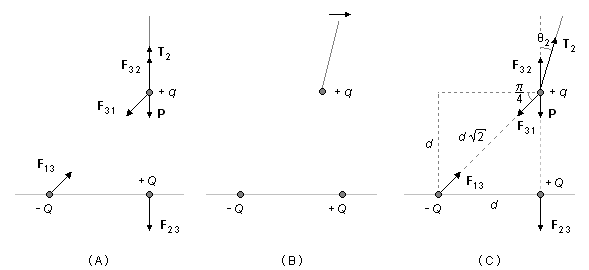
La force entre les charges +q et −Q, F31, agit le long de la diagonale du carré. Selon la Loi de Coulomb, le module de cette force sera
\[
\begin{gather}
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_1|}{r^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q||-Q|}{\left(d\sqrt{2\;}\right)^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2} \tag{V}
\end{gather}
\]
La force entre les charges +q et +Q, F32, sera
\[
\begin{gather}
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_2|}{r^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q||Q|}{d^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2} \tag{VI}
\end{gather}
\]
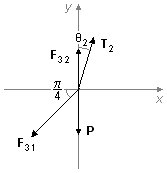
Comme la sphère est en équilibre, la somme des forces qui agissent sur elle est nulle. En
appliquant cette condition à la situation 2 (Figure 5)
\( \mathbf F_{32}=F_{32}\;\mathbf j \)
\( \mathbf T_2=T_2\sin\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\cos\dfrac{\pi}{4}\;\mathbf i-F_{31}\sin\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
\[
\begin{gather}
\mathbf F_{32}+\mathbf T_1+\mathbf F_{31}+\mathbf P=0
\end{gather}
\]
oú
\( \mathbf F_{32}=F_{32}\;\mathbf j \)
\( \mathbf T_2=T_2\sin\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\cos\dfrac{\pi}{4}\;\mathbf i-F_{31}\sin\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
en substituant les valeurs de (V) et (VI)
\[
\begin{gather}
F_{32}\;\mathbf j+T_2\sin\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j-F_{31}\cos\frac{\pi}{4}\;\mathbf i+F_{31}\sin\frac{\pi}{4}\;\mathbf j-mg\;\mathbf j=0\\[5pt]
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\;\mathbf j+T_2\sin\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf i-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf j-mg\;\mathbf j=0
\end{gather}
\]
en séparant les composantes
- Direction i:
\[
\begin{gather}
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}+T_2\sin\theta_2=0\\[5pt]
T_2\sin\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4} \tag{VII}
\end{gather}
\]
- Direction j:
\[
\begin{gather}
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}+T_2\cos\theta_2-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}-mg=0\\[5pt]
T_2\cos\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4}-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}+mg\\[5pt]
T_2\cos\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\left(\frac{\sqrt{2\;}}{4}-1\right)+mg \tag{VIII}
\end{gather}
\]
En divisant l'équation (IV) par l'équation (III) :
\[
\begin{gather}
\frac{T_1\cos\theta_1}{T_1\sin\theta_1}=\frac{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\left(1-\dfrac{\sqrt{2\;}}{4}\right)+mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_1}=\frac{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\left(1-\dfrac{\sqrt{2\;}}{4}\right)}{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\dfrac{\sqrt{2\;}}{4}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_1}=\left(1-\frac{\sqrt{2\;}}{4}\right)\frac{4}{\sqrt{2\;}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_1}=\left(\frac{4}{\sqrt{2\;}}-\frac{\cancel{\sqrt{2\;}}}{\cancel{4}}\frac{\cancel{4}}{\cancel{\sqrt{2\;}}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_1}=\left(\frac{4}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}-1\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_1}=\left(\frac{4\sqrt{2\;}}{2}-1\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}=\left(2\sqrt{2\;}-1\right)-\frac{1}{\tan\theta_1} \tag{IX}
\end{gather}
\]
En divisant l'équation (VIII) par l'équation (VII)
\[
\begin{gather}
\frac{T_2\cos\theta_2}{T_2\sin\theta_2}=\frac{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\left(\dfrac{\sqrt{2\;}}{4}-1\right)+mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_2}=\frac{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\left(\dfrac{\sqrt{2\;}}{4}-1\right)}{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\dfrac{\sqrt{2\;}}{4}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_2}=\left(\frac{\sqrt{2\;}}{4}-1\right)\frac{4}{\sqrt{2\;}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_2}=\left(\frac{\cancel{\sqrt{2\;}}}{\cancel{4}}\frac{\cancel{4}}{\cancel{\sqrt{2\;}}}-\frac{4}{\sqrt{2\;}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_2}=\left(1-\frac{4}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\tan\theta_2}=\left(1-\frac{4\sqrt{2\;}}{2}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}=\left(1-2\sqrt{2\;}\right)-\frac{1}{\tan\theta_2} \tag{X}
\end{gather}
\]
En égalisant les équations (IX) et (X)
\[
\begin{gather}
\left(2\sqrt{2\;}-1\right)-\frac{1}{\tan\theta_1}=\left(1-2\sqrt{2\;}\right)-\frac{1}{\tan\theta_2}\\[5pt]
\frac{1}{\tan\theta_1}-\frac{1}{\tan\theta_2}=\left(2\sqrt{2\;}-1\right)-\left(1-2\sqrt{2\;}\right)\\[5pt]
\frac{1}{\tan\theta_1}-\frac{1}{\tan\theta_2}=2\sqrt{2\;}-1-1+2\sqrt{2\;}\\[5pt]
\frac{1}{\tan\theta_1}-\frac{1}{\tan\theta_2}=4\sqrt{2\;}-2\\[5pt]
\frac{1}{\tan\theta_1}-\frac{1}{\tan\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
En substituant la condition donnée dans le problème θ1 = 2θ2
\[
\begin{gather}
\frac{1}{\tan 2\theta_2}-\frac{1}{\tan\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
De la Trigonométrie
\[
\begin{gather}
\tan(a+b)=\frac{\tan a+\tan b}{1-\tan a\tan b}
\end{gather}
\]
en étant a = b = θ2
\[
\begin{gather}
\tan 2\theta_2=\frac{2\tan\theta_2}{1-\tan^2\theta_2}
\end{gather}
\]
\[
\begin{gather}
\frac{1}{\dfrac{2\tan\theta_2}{1-\tan^2\theta_2}}-\frac{1}{\tan\theta_2}=2\left(2\sqrt{2\;}-1\right)\\[5pt]
\frac{1-\tan^2\theta_2}{2\tan\theta_2}-\frac{1}{\tan\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
en multipliant toute l'équation par 2 tan θ2
\[
\begin{gather}
\qquad \qquad \qquad \frac{1-\tan^2\theta_2}{2\tan\theta_2}-\frac{1}{\tan\theta_2}=2\left(2\sqrt{2\;}-1\right)\qquad (\times\;2\tan\theta_2)\\[5pt]
\frac{1-\tan^2\theta_2}{\cancel{2\tan\theta_2}}\cancel{2\tan\theta_2}-\frac{1}{\cancel{\tan\theta_2}}2\cancel{\tan\theta_2}=2\left(2\sqrt{2\;}-1\right)2\tan\theta_2\\[5pt]
1-\tan^2\theta_2-2=4\left(2\sqrt{2\;}-1\right)\tan\theta_2\\[5pt]
-\tan^2\theta_2-1=4\left(2\sqrt{2\;}-1\right)\tan\theta_2\\[5pt]
\tan^2\theta_2+4\left(2\sqrt{2\;}-1\right)\tan\theta_2+1=0
\end{gather}
\]
en effectuant un changement de variable x = tan θ2, nous pouvons réécrire
l'équation ci-dessus
\[
\begin{gather}
x^2+4\left(2\sqrt{2\;}-1\right)x+1=0
\end{gather}
\]
Solution de l'Équation du Second Degré \( x^2+4\left(2\sqrt{2\;}-1\right)x+1=0 \)
\[
\begin{array}{l}
\Delta =\left[4(2\sqrt{2\;}-1)\right]^2-4\times 1\times 1\\
\Delta =16(2\sqrt{2\;}-1)^2-4\\
\Delta=16(8-4\sqrt{2\;}+1)-4\\
\Delta =4(35-16\sqrt{2\;})\\[10pt]
x=\dfrac{-4(2\sqrt{2\;}-1)\pm\sqrt{4(35-16\sqrt{2\;})\;}}{2\times 1}
\end{array}
\]
les deux racines de l'équation seront
\[
\begin{gather}
x_1=-0,1394
\\ \quad \text{e} \quad \\
x_2=-7,1743
\end{gather}
\]
pour x1, nous aurons θ2 donné par
\[
\begin{gather}
\tan\theta_2=-0,1394\\[5pt]
\theta_2=\arctan(-0,1394)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_2=7,94°=7°56'}
\end{gather}
\]
selon la condition du problème, nous avons pour θ1
\[
\begin{gather}
\theta_1=2\times 7,94
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_1=15,88°=15°52'}
\end{gather}
\]
pour x2, nous aurons θ2 donné par
\[
\begin{gather}
\tan\theta_2=-7,1743\\[5pt]
\theta_2=\arctan(-7,1743)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_2=82,06°=82°03'}
\end{gather}
\]
selon la condition du problème, nous avons pour θ1
\[
\begin{gather}
\theta_1=2\times 82,06
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_1=164,12°=164°04'}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .