Ejercicio Resuelto sobre Fuerza Eléctrica
publicidad
Dos cargas con el mismo módulo y signos opuestos están fijas sobre una línea horizontal a una distancia d una de la otra. Una esfera, de masa m cargada con una carga eléctrica, y sujeta a un hilo es aproximada. primero a una de las cargas hasta que queda en equilibrio exactamente sobre esta, a una altura d de la misma. A continuación, el hilo se desplaza en dirección a la segunda carga hasta que la carga queda en equilibrio sobre la segunda carga. Encontrar los ángulos de desviación del hilo en ambas situaciones, sabiendo que sobre la primera carga el ángulo de desviación es el doble del ángulo de desviación sobre la segunda carga.
Datos del problema:
- Distancia entre las cargas en la horizontal: d;
- Distancia entre las cargas en la vertical: d;
- Masa de la esfera: m;
- Relación entre los ángulos de desviación: θ1 = 2θ2.
Adoptamos que las cargas fijas, 1 y 2 en la Figura 1, tienen valor −Q y +Q y la carga suspendida por el hilo tiene carga +q (carga 3).
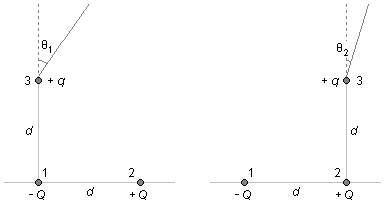
En las situaciones de equilibrio, tenemos una distancia d entre las cargas fijas en la horizontal, y la carga suspendida está a una distancia d en la vertical. El ángulo θ1 es el doble de θ2, según los datos del problema.
Solución:
Inicialmente, la carga +q es aproximada a la primera carga −Q en la vertical. En la carga +q actúa el peso P, la fuerza de tensión T1, la fuerza eléctrica de atracción entre +q y −Q, F31, y la fuerza eléctrica de repulsión entre +q y +Q, F32 (Figura 2-A). Las fuerzas en la vertical se equilibran, quedando solo la componente horizontal de la fuerza de repulsión F32, que desplaza la carga +q de la posición de equilibrio. Para restablecer el equilibrio, debe desplazarse hacia la derecha (Figura 2-B) hasta quedar en la vertical sobre la carga −Q; en este instante, el hilo que sostiene la carga +q forma un ángulo θ1 con la vertical (Figura 2-C).
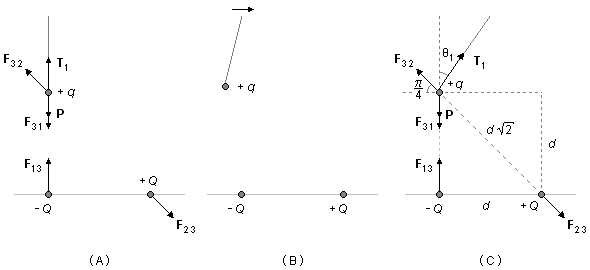
La fuerza entre las cargas +q y −Q, F31, actúa a lo largo del lado del cuadrado que mide d. Según la Ley de Coulomb, el módulo de esta fuerza será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{el}=\frac{1}{4\pi\varepsilon_0}\frac{|q_{\small A}||q_{\small B}|}{r^2}}
\end{gather}
\]
\[
\begin{gather}
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_1|}{r^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q||-Q|}{d^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2} \tag{I}
\end{gather}
\]
La fuerza entre las cargas +q y +Q, F32, actúa a lo largo de la diagonal de
un cuadrado de lado d, formado por la distancia entre las cargas +Q y −Q y la
altura de la carga +q; la diagonal mide
\( d\sqrt{2\;} \)
y esta fuerza forma un ángulo
\( \frac{\pi}{4} \)
con la horizontal, y su módulo será
\[
\begin{gather}
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_2|}{r^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q||Q|}{\left(d\sqrt{2\;}\right)^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2} \tag{II}
\end{gather}
\]
Como la esfera está en equilibrio, la suma de las fuerzas que actúan sobre ella es igual
a cero
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum \mathbf F=0}
\end{gather}
\]
aplicando esta condición a la situación 1 (Figura 3)
\[
\begin{gather}
\mathbf F_{32}+\mathbf T_1+\mathbf F_{31}+\mathbf P=0
\end{gather}
\]
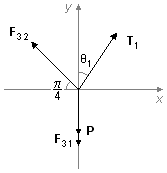
donde
\( \mathbf F_{32}=-F_{32}\cos\dfrac{\pi}{4}\;\mathbf i+F_{32}\operatorname{sen}\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf T_1=T_1\operatorname{sen}\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
sustituyendo los valores de (I) y (II)
\[
\begin{gather}
-F_{32}\cos\frac{\pi}{4}\;\mathbf i+F_{32}\operatorname{sen}\frac{\pi}{4}\;\mathbf j+T_1\operatorname{sen}\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j-F_{31}\;\mathbf j-mg\;\mathbf j=0\\[5pt]
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}\;\mathbf i+\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf j+T_1\operatorname{sen}\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\;\mathbf j-mg\;\mathbf j=0
\end{gather}
\]
separando los componentes
- Dirección i:
\[
\begin{gather}
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}+T_1\operatorname{sen}\theta_1=0\\[5pt]
T_1\operatorname{sen}\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4} \tag{III}
\end{gather}
\]
- Dirección j:
\[
\begin{gather}
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}+T_1\cos\theta_1-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}-mg=0\\[5pt]
T_1\cos\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4}+mg\\[5pt]
T_1\cos\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\left(1-\frac{\sqrt{2\;}}{4}\right)+mg \tag{IV}
\end{gather}
\]
De la misma manera, en el segundo caso, la carga +q es aproximada a la segunda carga +Q en la
vertical. En la carga +q actúan el peso P, la fuerza de tensión en el hilo
T2, la fuerza de atracción entre +q y −Q, F31, y la
fuerza de repulsión entre +q y +Q, F32 (Figura 4-A). Las fuerzas en la
vertical se equilibran, quedando solo la componente horizontal de la fuerza de atracción
F31 que desplaza la carga +q de la posición de equilibrio. Para restablecer el
equilibrio, debe desplazarse hacia la derecha (Figura 4-B) hasta quedar en la vertical sobre la carga
+Q. En este instante, el hilo que sostiene la carga +q forma un ángulo
θ2 con la vertical (Figura 4-C).
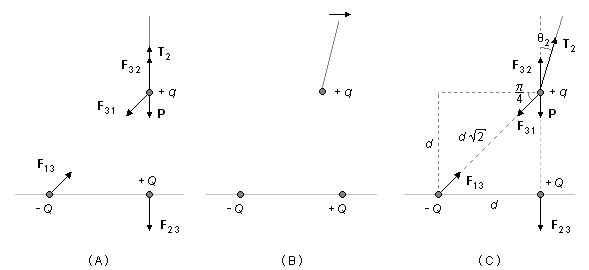
La fuerza entre las cargas +q y −Q, F31, actúa a lo largo de la diagonal del cuadrado. Según la Ley de Coulomb, el módulo de esta fuerza será
\[
\begin{gather}
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_1|}{r^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q||-Q|}{\left(d\sqrt{2\;}\right)^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2} \tag{V}
\end{gather}
\]
La fuerza entre las cargas +q y +Q, F32, será
\[
\begin{gather}
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_2|}{r^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q||Q|}{d^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2} \tag{VI}
\end{gather}
\]
Como la esfera está en equilibrio, la suma de las fuerzas que actúan sobre ella es cero,
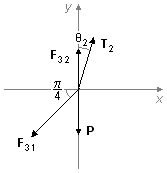
aplicando esta condición a la situación 2 (Figura 5)
\( \mathbf F_{32}=F_{32}\;\mathbf j \)
\( \mathbf T_2=T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\cos\dfrac{\pi}{4}\;\mathbf i-F_{31}\operatorname{sen}\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
\[
\begin{gather}
\mathbf F_{32}+\mathbf T_1+\mathbf F_{31}+\mathbf P=0
\end{gather}
\]
donde
\( \mathbf F_{32}=F_{32}\;\mathbf j \)
\( \mathbf T_2=T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\cos\dfrac{\pi}{4}\;\mathbf i-F_{31}\operatorname{sen}\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
sustituyendo los valores de (V) y (VI)
\[
\begin{gather}
F_{32}\;\mathbf j+T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j-F_{31}\cos\frac{\pi}{4}\;\mathbf i+F_{31}\operatorname{sen}\frac{\pi}{4}\;\mathbf j-mg\;\mathbf j=0\\[5pt]
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\;\mathbf j+T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf i-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf j-mg\;\mathbf j=0
\end{gather}
\]
separando los componentes
- Dirección i:
\[
\begin{gather}
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}+T_2\operatorname{sen}\theta_2=0\\[5pt]
T_2\operatorname{sen}\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4} \tag{VII}
\end{gather}
\]
- Dirección j:
\[
\begin{gather}
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}+T_2\cos\theta_2-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}-mg=0\\[5pt]
T_2\cos\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4}-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}+mg\\[5pt]
T_2\cos\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\left(\frac{\sqrt{2\;}}{4}-1\right)+mg \tag{VIII}
\end{gather}
\]
Dividiendo la ecuación (IV) por la ecuación (III)
\[
\begin{gather}
\frac{T_1\cos\theta_1}{T_1\operatorname{sen}\theta_1}=\frac{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\left(1-\dfrac{\sqrt{2\;}}{4}\right)+mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\frac{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\left(1-\dfrac{\sqrt{2\;}}{4}\right)}{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\dfrac{\sqrt{2\;}}{4}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(1-\frac{\sqrt{2\;}}{4}\right)\frac{4}{\sqrt{2\;}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(\frac{4}{\sqrt{2\;}}-\frac{\cancel{\sqrt{2\;}}}{\cancel{4}}\frac{\cancel{4}}{\cancel{\sqrt{2\;}}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(\frac{4}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}-1\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(\frac{4\sqrt{2\;}}{2}-1\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}=\left(2\sqrt{2\;}-1\right)-\frac{1}{\operatorname{tg}\theta_1} \tag{IX}
\end{gather}
\]
Dividiendo la ecuación (VIII) por la ecuación (VII)
\[
\begin{gather}
\frac{T_2\cos\theta_2}{T_2\operatorname{sen}\theta_2}=\frac{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\left(\dfrac{\sqrt{2\;}}{4}-1\right)+mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\frac{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\left(\dfrac{\sqrt{2\;}}{4}-1\right)}{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\dfrac{\sqrt{2\;}}{4}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(\frac{\sqrt{2\;}}{4}-1\right)\frac{4}{\sqrt{2\;}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(\frac{\cancel{\sqrt{2\;}}}{\cancel{4}}\frac{\cancel{4}}{\cancel{\sqrt{2\;}}}-\frac{4}{\sqrt{2\;}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(1-\frac{4}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(1-\frac{4\sqrt{2\;}}{2}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}=\left(1-2\sqrt{2\;}\right)-\frac{1}{\operatorname{tg}\theta_2} \tag{X}
\end{gather}
\]
Igualando las ecuaciones (IX) y (X)
\[
\begin{gather}
\left(2\sqrt{2\;}-1\right)-\frac{1}{\operatorname{tg}\theta_1}=\left(1-2\sqrt{2\;}\right)-\frac{1}{\operatorname{tg}\theta_2}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=\left(2\sqrt{2\;}-1\right)-\left(1-2\sqrt{2\;}\right)\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=2\sqrt{2\;}-1-1+2\sqrt{2\;}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=4\sqrt{2\;}-2\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
Sustituyendo la condición dada en el problema θ1 = 2θ2
\[
\begin{gather}
\frac{1}{\operatorname{tg}2\theta_2}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
De la Trigonometría
\[
\begin{gather}
\operatorname{tg}(a+b)=\frac{\operatorname{tg}a+\operatorname{tg}b}{1-\operatorname{tg}a\operatorname{tg}b}
\end{gather}
\]
siendo a = b = θ2
\[
\begin{gather}
\operatorname{tg}2\theta_2=\frac{2\operatorname{tg}\theta_2}{1-\operatorname{tg}^2\theta_2}
\end{gather}
\]
\[
\begin{gather}
\frac{1}{\dfrac{2\operatorname{tg}\theta_2}{1-\operatorname{tg}^2\theta_2}}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)\\[5pt]
\frac{1-\operatorname{tg}^2\theta_2}{2\operatorname{tg}\theta_2}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
multiplicando toda la ecuación por 2 tg θ2
\[
\begin{gather}
\qquad \qquad \qquad \frac{1-\operatorname{tg}^2\theta_2}{2\operatorname{tg}\theta_2}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)\qquad (\times\;2\operatorname{tg}\theta_2)\\[5pt]
\frac{1-\operatorname{tg}^2\theta_2}{\cancel{2\operatorname{tg}\theta_2}}\cancel{2\operatorname{tg}\theta_2}-\frac{1}{\cancel{\operatorname{tg}\theta_2}}2\cancel{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)2\operatorname{tg}\theta_2\\[5pt]
1-\operatorname{tg}^2\theta_2-2=4\left(2\sqrt{2\;}-1\right)\operatorname{tg}\theta_2\\[5pt]
-\operatorname{tg}^2\theta_2-1=4\left(2\sqrt{2\;}-1\right)\operatorname{tg}\theta_2\\[5pt]
\operatorname{tg}^2\theta_2+4\left(2\sqrt{2\;}-1\right)\operatorname{tg}\theta_2+1=0
\end{gather}
\]
haciendo el cambio de variable x = tg θ2, podemos reescribir la ecuación
anterior
\[
\begin{gather}
x^2+4\left(2\sqrt{2\;}-1\right)x+1=0
\end{gather}
\]
Solución de la Ecuación de Segundo Grado \( x^2+4\left(2\sqrt{2\;}-1\right)x+1=0 \)
\[
\begin{array}{l}
\Delta =\left[4(2\sqrt{2\;}-1)\right]^2-4\times 1\times 1\\
\Delta =16(2\sqrt{2\;}-1)^2-4\\
\Delta=16(8-4\sqrt{2\;}+1)-4\\
\Delta =4(35-16\sqrt{2\;})\\[10pt]
x=\dfrac{-4(2\sqrt{2\;}-1)\pm\sqrt{4(35-16\sqrt{2\;})\;}}{2\times 1}
\end{array}
\]
las dos raíces de la ecuación serán
\[
\begin{gather}
x_1=-0,1394
\\ \quad \text{e} \quad \\
x_2=-7,1743
\end{gather}
\]
para x1 tendremos θ2 dado por
\[
\begin{gather}
\operatorname{tg}\theta_2=-0,1394\\[5pt]
\theta_2=\operatorname{arctg}(-0,1394)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_2=7,94°=7°56'}
\end{gather}
\]
de la condición del problema tenemos para θ1
\[
\begin{gather}
\theta_1=2\times 7,94
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_1=15,88°=15°52'}
\end{gather}
\]
para x2 tendremos θ2 dado por
\[
\begin{gather}
\operatorname{tg}\theta_2=-7,1743\\[5pt]
\theta_2=\operatorname{arctg}(-7,1743)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_2=82,06°=82°03'}
\end{gather}
\]
de la condición del problema tenemos para θ1
\[
\begin{gather}
\theta_1=2\times 82,06
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_1=164,12°=164°04'}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .