Exercice Résolu sur les Champ Électrique
publicité
Deux charges égales de même signe sont séparées par une distance 2d. Calculer le vecteur champ électrostatique aux points loin de la médiatrice de la droite reliant les deux charges. Vérifiez la solution pour des points loin du centre du système.
Schéma du problème:
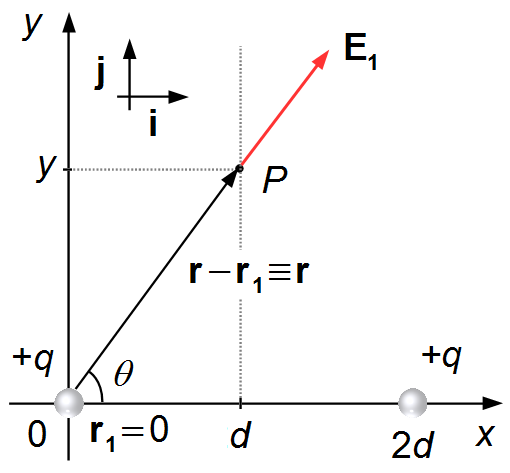
Le vecteur r localise le point P, où nous voulons calculer le champ électrique par rapport
à l'origine, et est noté
\( \mathbf r=d\;\mathbf i+y\;\mathbf j \).
Le vecteur r1 va de l'origine jusqu'à la charge +q (Figure 1), comme la charge
est située à l'origine, ce vecteur est nul,
\( \mathbf r_1=\mathbf{0} \).
Le vecteur r−r1 va de la charge jusqu'au point P, dans ce cas il
coïncide avec le vecteur r, et est noté
\( \mathbf r-\mathbf r_1=d\;\mathbf i+y\;\mathbf j-\mathbf{0}=d\;\mathbf i+y\;\mathbf j \).
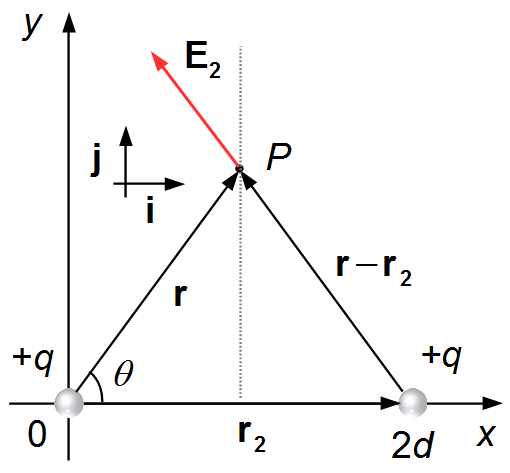
Le vecteur r est le même que dans la situation précédente. Le vecteur r2 va de
l'origine jusqu'à la deuxième charge +q, et est noté
\( \mathbf r_2=2d\mathbf i \).
Le vecteur r−r2 va de la charge jusqu'au point P, et est noté
\( \mathbf r-\mathbf r_2=d\;\mathbf i+y\;\mathbf j-2d\mathbf i=-d\;\mathbf i+y\;\mathbf j \),
(Figure 2).
Solution:
Le vecteur champ électrostatique d'un système discret de charges est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\;\sum_{i=1}^n\;\frac{q_i}{\left|\mathbf r-\mathbf r_i\right|^2}\;\frac{\mathbf r-\mathbf r_i}{\left|\mathbf r-\mathbf r_i\right|}}
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\left\{\frac{q_1}{\left|\mathbf r-\mathbf r_1\right|^2}\;\frac{\mathbf r-\mathbf r_1}{\left|\mathbf r-\mathbf r_1\right|}+\frac{q_2}{\left|\mathbf r-\mathbf r_2\right|^2}\;\frac{\mathbf r-\mathbf r_2}{\left|\mathbf r-\mathbf r_2\right|}\right\}
\end{gather}
\]
Les dénominateurs de l'équation ci-dessus sont écrits comme (Figures 1 et 2):
\( \left|\mathbf r-\mathbf r_1\right|=\sqrt{d^2+y^2\;} \)
\( \left|\mathbf r-\mathbf r_1\right|^2=d^2+y^2 \)
\( \left|\mathbf r-\mathbf r_2\right|=\sqrt{(-d)^2+y^2\;}=\sqrt{d^2+y^2\;} \)
\( \left|\mathbf r-\mathbf r_2\right|^2=d^2+y^2 \)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\left\{\frac{q}{\left(d^2+y^2\right)^{1/2}}\;\frac{\left(d\;\mathbf i+y\;\mathbf j\right)}{\left(d^2+y^2\right)}+\frac{q}{\left(d^2+y^2\right)^{1/2}}\;\frac{\left(-d\;\mathbf i+y\;\mathbf j\right)}{\left(d^2+y^2\right)}\right\}\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{q}{\left(d^2+y^2\right)^{3/2}}\left[d\;\mathbf i+y\;\mathbf j-d\;\mathbf i-y\;\mathbf j\right]\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2yq}{\left(d^2+y^2\right)^{3/2}}\;\mathbf j
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{\left(d^2+y^2\right)^{3/2}}\;\mathbf j}
\end{gather}
\]
Pour des points loin du centre du système, avec y≫d, nous pouvons négliger le terme en
d2 au dénominateur et la solution sera
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{\left(\cancel{d^2}+y^2\right)^{3/2}}\;\mathbf j\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{y^{\cancel 2\times\frac{3}{\cancel 2}}}\;\mathbf j\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2q\cancel y}{y^{\cancelto{2}{3}}}\;\mathbf j\\[5pt]
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2q}{y^2}\;\mathbf j}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .