Ejercicio Resuelto sobre Campo Eléctrico
publicidad
Dos cargas iguales del mismo signo están separadas por una distancia 2d. Calcule el vector campo eléctrico en los puntos a lo largo de la mediatriz de la línea que une las dos cargas. Verifique la solución para puntos muy alejados del centro del sistema.
Esquema del problema:
El vector r localiza el punto P, donde queremos calcular el campo eléctrico en relación con
el origen, y se escribe como,
\( \mathbf r=d\;\mathbf i+y\;\mathbf j \).
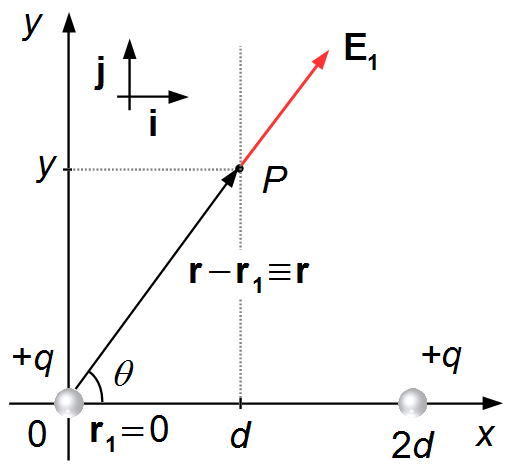
El vector r1 va desde el origen hasta la carga +q (Figura 1), como la carga está
localizada en el origen, este vector es igual a cero,
\( \mathbf r_1=\mathbf{0} \).
El vector r−r1 va desde la carga hasta el punto P, en este caso
coincide con el vector r, y se da por
\( \mathbf r-\mathbf r_1=d\;\mathbf i+y\;\mathbf j-\mathbf{0}=d\;\mathbf i+y\;\mathbf j \).
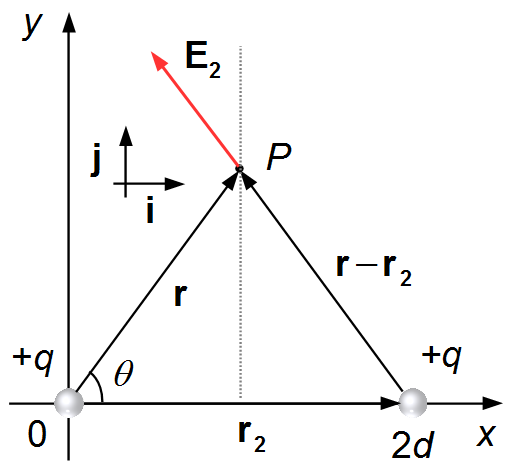
El vector r es el mismo que en la situación anterior. El vector r2 va desde el
origen hasta la segunda carga +q, y se da por
\( \mathbf r_2=2d\mathbf i \).
El vector r−r2 va desde la carga hasta el punto P, y se da por
\( \mathbf r-\mathbf r_2=d\;\mathbf i+y\;\mathbf j-2d\mathbf i=-d\;\mathbf i+y\;\mathbf j \),
(Figura 2).
Solución:
El vector campo eléctrico de un sistema discreto de cargas se da por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\;\sum_{i=1}^n\;\frac{q_i}{\left|\mathbf r-\mathbf r_i\right|^2}\;\frac{\mathbf r-\mathbf r_i}{\left|\mathbf r-\mathbf r_i\right|}}
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\left\{\frac{q_1}{\left|\mathbf r-\mathbf r_1\right|^2}\;\frac{\mathbf r-\mathbf r_1}{\left|\mathbf r-\mathbf r_1\right|}+\frac{q_2}{\left|\mathbf r-\mathbf r_2\right|^2}\;\frac{\mathbf r-\mathbf r_2}{\left|\mathbf r-\mathbf r_2\right|}\right\}
\end{gather}
\]
Los denominadores de la ecuación anterior se escriben como (Figuras 1 y 2):
\( \left|\mathbf r-\mathbf r_1\right|=\sqrt{d^2+y^2\;} \)
\( \left|\mathbf r-\mathbf r_1\right|^2=d^2+y^2 \)
\( \left|\mathbf r-\mathbf r_2\right|=\sqrt{(-d)^2+y^2\;}=\sqrt{d^2+y^2\;} \)
\( \left|\mathbf r-\mathbf r_2\right|^2=d^2+y^2 \)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\left\{\frac{q}{\left(d^2+y^2\right)^{1/2}}\;\frac{\left(d\;\mathbf i+y\;\mathbf j\right)}{\left(d^2+y^2\right)}+\frac{q}{\left(d^2+y^2\right)^{1/2}}\;\frac{\left(-d\;\mathbf i+y\;\mathbf j\right)}{\left(d^2+y^2\right)}\right\}\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{q}{\left(d^2+y^2\right)^{3/2}}\left[d\;\mathbf i+y\;\mathbf j-d\;\mathbf i-y\;\mathbf j\right]\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2yq}{\left(d^2+y^2\right)^{3/2}}\;\mathbf j
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{\left(d^2+y^2\right)^{3/2}}\;\mathbf j}
\end{gather}
\]
Para puntos muy alejados del centro del sistema, tenemos y≫d, podemos despreciar el término
en d2 en el denominador y la solución será
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{\left(\cancel{d^2}+y^2\right)^{3/2}}\;\mathbf j\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{y^{\cancel 2\times\frac{3}{\cancel 2}}}\;\mathbf j\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2q\cancel y}{y^{\cancelto{2}{3}}}\;\mathbf j\\[5pt]
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2q}{y^2}\;\mathbf j}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .