Exercice Résolu sur les Statique
publicité
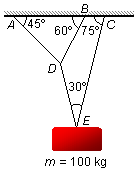
Un bloc de masse m = 100 kg est suspendu par le système de cordes montré dans la figure.
Déterminer les forces de tension dans toutes les cordes.
Données \( \sin 15°=0,259 \), \( \cos 15°=0,966 \), \( \sin 45°=0,707 \), \( \cos 45°=0,707 \), \( \sin 60°=0,866 \), \( \cos 60°=0,5 \).
Données \( \sin 15°=0,259 \), \( \cos 15°=0,966 \), \( \sin 45°=0,707 \), \( \cos 45°=0,707 \), \( \sin 60°=0,866 \), \( \cos 60°=0,5 \).
Données du problème:
- Masse du bloc: m=100 kg;
- Accélération de la pesanteur: g=9,8 m/s2.
Dessiner les forces agissant sur le système.
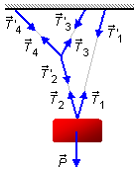
Sur le bloc, le poids \( \vec P \) est équilibrée par la force de tension \( {\vec T}_1 \), qui a pour force de réaction \( {\vec T}\text{'}_1 \) au plafond, et par la force de tension \( {\vec T}_2 \), qui a pour force de réaction \( {\vec T}\text{'}_2 \) appliquée au point D.
Au point D, la force de tension \( {\vec T}\text{'}_2 \) est équilibrée par les forces de tension \( {\vec T}_3 \) et \( {\vec T}_4 \), qui ont pour forces de réaction \( {\vec T}\text{'}_3 \) et \( {\vec T}\text{'}_4 \) au plafond.
Sur le bloc, le poids \( \vec P \) est équilibrée par la force de tension \( {\vec T}_1 \), qui a pour force de réaction \( {\vec T}\text{'}_1 \) au plafond, et par la force de tension \( {\vec T}_2 \), qui a pour force de réaction \( {\vec T}\text{'}_2 \) appliquée au point D.
Au point D, la force de tension \( {\vec T}\text{'}_2 \) est équilibrée par les forces de tension \( {\vec T}_3 \) et \( {\vec T}_4 \), qui ont pour forces de réaction \( {\vec T}\text{'}_3 \) et \( {\vec T}\text{'}_4 \) au plafond.
Solution:
Comme le système est en équilibre, la résultante des forces est nulle et nous appliquons la condition
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum F=0} \tag{I}
\end{gather}
\]
En divisant le problème en deux parties, premiérement, en etudiant les forces sur le bloc.
Du point C, nous traçons une ligne verticale perpendiculaire au plafond. L'angle entre le plafond et la corde \( \overline{CE} \) est de 75°, donc l'angle entre la ligne tracée et la corde \( \overline{CE} \) est de 15°, ce sont des angles complémentaires qui totalisent 90° (Figure 2-A).
À partir du bloc au point E, nous traçons une ligne verticale divisant l'angle de 30° en deux parties. Comme l'angle entre cette ligne et la corde \( \overline{CE} \) est alterné-interne avec l'angle trouvé précédemment, il mesurera également 15°. Cette ligne divise l'angle de 30° en deux parties égales, c'est la bissectrice de l'angle de 30°.
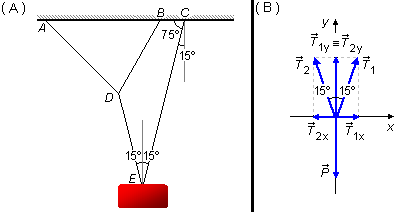
Dessiner les forces agissant sur le bloc (Figure 2-B) dans un système de coordonnées xy et décomposer les forces. Le poids \( \vec P \) n'a qu'une composante dans la direction y, les forces de tension \( {\vec T}_1 \) et \( {\vec T}_2 \) ont des composantes \( {\vec T}_{1x} \) et \( {\vec T}_{2x} \) dans la direction x et des composantes \( {\vec T}_{1y} \) et \( {\vec T}_{2y} \) dans la direction y.
\[
\begin{gather}
{\vec T}_1+{\vec T}_2+\vec P=0 \\[5pt]
{\vec T}_{1x}+{\vec T}_{1y}-{\vec T}_{2x}+{\vec T}_{2y}-\vec P=0 \tag{II}
\end{gather}
\]
- Direction x:
\[
T_{1x}=T_1\sin 15° \tag{III}
\]
\[
T_{2x}=T_2\sin 15° \tag{IV}
\]
Remarque: contrairement à ce qui est habituellement fait, où l'angle est mesuré par rapport
à l'axe x et la composante dans cette direction est proportionnelle au cosinus, l'angle a été mesuré
par rapport à l'axe y et la composante est proportionnelle au sinus de l'angle.
- Direction y:
\[
T_{1y}=T_1\cos 15° \tag{V}
\]
\[
T_{2y}=T_2\cos 15° \tag{VI}
\]
Le poids est donnée par
A força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{VII}
\end{gather}
\]
En substituant les équations (III), (IV), (V), (VI) et (VII) dans l'équation (II) et en séparant les
composantes dans les directions x et y.
- Direction x:
\[
\begin{gather}
T_1\sin 15°-T_2\sin 15°=0
\end{gather}
\]
- Direction y:
\[
\begin{gather}
T_1\cos 15°+T_2\cos 15°-mg=0
\end{gather}
\]
ces équations forment un système de deux équations à deux inconnues (T1 et
T2)
\[
\begin{gather}
\left\{
\begin{array}{l}
T_1\sin 15°-T_2\sin 15°=0\\
T_1\cos 15°+T_2\cos 15°-P=0
\end{array}
\right.
\end{gather}
\]
en isolant T1 dans la première équation du système
\[
\begin{gather}
T_1\sin 15°-T_2\sin 15°=0 \\[5pt]
T_1\cancel{\sin 15°}=T_2\cancel{\sin 15°} \\[5pt]
T_1=T_2 \tag{VIII}
\end{gather}
\]
en substituant la valeur de (VIII) dans la deuxième équation du système
\[
\begin{gather}
T_2\cos 15°+T_2\cos 15°-mg=0 \\[5pt]
2 T_2\cos 15°=mg \\[5pt]
T_2=\frac{mg}{2\cos 15°}
\end{gather}
\]
en substituant les données du problème
\[
\begin{gather}
T_2=\frac{100\times 9,8}{2\times 0,966} \\[5pt]
T_2=507,3
\end{gather}
\]
par l'égalité (VII)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_1=T_2=507,3\;\mathrm N}
\end{gather}
\]
Étudions les forces agissant au point D.
En traçant une ligne horizontale passant par le point D, l'angle entre cette ligne et la corde \( \overline{AD} \) est de 45º, c'est un angle alterné interne avec l'angle entre la corde \( \overline{AD} \) et le plafond (Figure 3-A).
L'angle entre la corde \( \overline{BD} \) et la ligne horizontale est de 60º, c'est un angle alterné interne avec l'angle entre la corde \( \overline{BD} \) et le plafond.
En traçant une ligne verticale passant par le point D, l'angle entre la corde \( \overline{DE} \) et cette ligne est de 15º, c'est un angle alterné interne avec l'angle trouvé dans la première partie du problème.
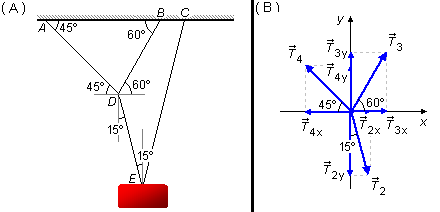
Dessiner les forces au point D (Figure 3-B) dans un système de coordonnées xy et décomposer les forces. La force de tension \( {\vec T}_2 \) a déjà été déterminée, avec des composantes \( {\vec T}_{2x} \) et \( {\vec T}_{2y} \). Les forces de tension \( {\vec T}_3 \) et \( {\vec T}_4 \) ont des composantes \( {\vec T}_{3x} \) et \( {\vec T}_{4x} \) dans la direction x et des composantes \( {\vec T}_{3y} \) et \( {\vec T}_{4y} \) dans la direction y.
Comme le système est en équilibre, nous pouvons appliquer la condition (I)
\[
\begin{gather}
{\vec T}_2+{\vec T}_3+{\vec T}_4=0 \\[5pt]
{\vec T}_{2x}-{\vec T}_{2y}+{\vec T}_{3x}+{\vec T}_{3y}-{\vec T}_{4x}+{\vec T}_{4y}=0 \tag{IX}
\end{gather}
\]
- Direction x:
\[
T_{2x}=T_2\sin 15° \tag{X}
\]
\[
T_{3x}=T_3\cos 60° \tag{XI}
\]
\[
T_{4x}=T_4\cos 45° \tag{XII}
\]
- Direction y:
\[
T_{2y}=T_2\cos 15° \tag{XIII}
\]
\[
T_{3y}=T_3\sin 60° \tag{XIV}
\]
\[
T_{4y}=T_4\sin 45° \tag{XV}
\]
En substituant les équations (X), (XI), (XII), (XIII), (XIV) et (XV) dans l'équation (IX) et en séparant les
composantes dans les directions x et y.
- Direction x:
\[
\begin{gather}
T_2\sin 15°+T_3\cos 60°-T_4\cos 45°=0\\[5pt]
\end{gather}
\]
- Direction y:
\[
\begin{gather}
T_3\sin 60°+T_4\sin 45°-T_2\cos 15°=0
\end{gather}
\]
ces équations forment un système de deux équations à deux inconnues (T3 et
T4)
Remarque: T2 n'est pas une inconnue, elle a déjà été déterminée auparavant,
nous passons donc les termes en T2 dans les deux équations du côté droit de l'égalité.
\[
\begin{gather}
&\left\{
\begin{matrix}
T_2\sin 15°+T_3\cos 60°-T_4\cos 45°=0\\
T_3\sin 60°+T_4\sin 45°-T_2\cos 15°=0
\end{matrix}
\right.\\[8pt]
&\left\{
\begin{matrix}
T_3\cos 60°-T_4\cos 45°=-T_2\sin 15°\\
T_3\sin 60°+T_4\sin 45°=T_2\cos 15°
\end{matrix}
\right.
\end{gather}
\]
en additionnant les deux équations du système, nous éliminons le terme en T4
\[
\begin{gather}
\frac{
\begin{matrix}
T_3\cos 60°-\cancel{T_4\cos 45°}=-T_2\sin 15°\\
T_3\sin 60°+\cancel{T_4\sin 45°}=T_2\cos 15°
\end{matrix}}
{T_3(\cos 60°+\sin 60°)+0=T_2(\cos 15°-\sin 15°)}\\[5pt]
T_3=\frac{\cos 15°-\sin 15°}{\cos 60°+\sin 60°}\,T_2
\end{gather}
\]
Remarque: n'oubliez pas que cos 45° est égal à sin 45°, donc ces termes se compensent
lorsque nous additionnons les deux équations, car ils ont des signes opposés dans les équations.
en substituant les valeurs données dans le problème et la tension T2 déterminée ci-dessus
\[
\begin{gather}
T_3=\frac{0,966-0,258}{0,500+0,866}\times 507,3
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_3=262,9\;\mathrm N}
\end{gather}
\]
En isolant T4 dans la deuxième équation du système
\[
\begin{gather}
T_3\sin 60°+T_4\sin 45°=T_2\cos 15° \\[5pt]
T_4=\frac{T_2\cos 15°-T_3\sin 60°}{\sin 45°}
\end{gather}
\]
en substituant les valeurs données dans le problème et les tensions T2 et
T3 déterminées ci-dessus
\[
\begin{gather}
T_4=\frac{507,3\times 0,966-262,9\times 0,866}{0,707}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_4=371,1\;\mathrm N}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .