Ejercicio Resuelto sobre Estática
publicidad
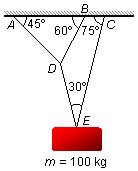
Un bloque de masa m = 100 kg está suspendido por el sistema de cuerdas mostrado en la figura.
Determinar las tensiones en todas las cuerdas.
Datos: \( \operatorname{sen}15°=0,259 \), \( \cos 15°=0,966 \), \( \operatorname{sen}45°=0,707 \), \( \cos 45°=0,707 \), \( \operatorname{sen}60°=0,866 \), \( \cos 60°=0,5 \).
Datos: \( \operatorname{sen}15°=0,259 \), \( \cos 15°=0,966 \), \( \operatorname{sen}45°=0,707 \), \( \cos 45°=0,707 \), \( \operatorname{sen}60°=0,866 \), \( \cos 60°=0,5 \).
Datos del problema:
- Masa del bloque: m=100 kg;
- Aceleración de la gravedad: g=9,8 m/s2.
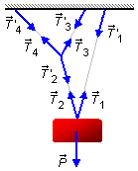
Dibujando las fuerzas que actúan en el sistema.
En el bloque, el peso \( \vec P \) es equilibrada por la tensión \( \vec P \), que tiene como reacción la fuerza \( {\vec T}\text{'}_1 \) en el techo, y por la tensión \( {\vec T}_2 \), que tiene como reacción la fuerza \( {\vec T}\text{'}_2 \) aplicada en el punto D.
En el punto D, la tensión \( {\vec T}\text{'}_2 \) está equilibrada por las tensión \( {\vec T}_3 \) y \( {\vec T}_4 \), que tienen como reacciones las fuerzas \( {\vec T}\text{'}_3 \) y \( {\vec T}\text{'}_4 \) en el techo.
En el bloque, el peso \( \vec P \) es equilibrada por la tensión \( \vec P \), que tiene como reacción la fuerza \( {\vec T}\text{'}_1 \) en el techo, y por la tensión \( {\vec T}_2 \), que tiene como reacción la fuerza \( {\vec T}\text{'}_2 \) aplicada en el punto D.
En el punto D, la tensión \( {\vec T}\text{'}_2 \) está equilibrada por las tensión \( {\vec T}_3 \) y \( {\vec T}_4 \), que tienen como reacciones las fuerzas \( {\vec T}\text{'}_3 \) y \( {\vec T}\text{'}_4 \) en el techo.
Solución:
Como el sistema está en equilibrio, la resultante de las fuerzas es nula y aplicamos la condición
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum F=0} \tag{I}
\end{gather}
\]
Dividiendo el problema en dos partes, primero estudiamos las fuerzas en el bloque.
Desde el punto C trazamos una línea vertical perpendicular al techo; el ángulo entre el techo y la cuerda \( \overline{CE} \) es de 75°, por lo que el ángulo entre la línea trazada y la cuerda \( \overline{CE} \) es de 15°, son ángulos complementarios y suman 90° (Figura 2-A).
Desde el bloque en el punto E trazamos una línea vertical que divide el ángulo de 30° en dos partes. Como el ángulo entre esta línea y la cuerda \( \overline{CE} \) es alterno interno con el ángulo encontrado anteriormente, también medirá 15°. Esta línea divide el ángulo de 30° en dos partes iguales, siendo una bisectriz del ángulo de 30°.
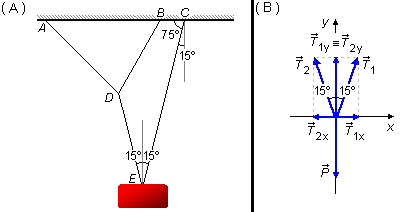
Dibujando las fuerzas que actúan en el bloque (Figura 2-B) en un sistema de coordenadas xy y descomponiendo las fuerzas. El peso \( \vec P \) tiene componente solo en la dirección y, las tensiones \( {\vec T}_1 \) y \( {\vec T}_2 \) tienen componentes \( {\vec T}_{1x} \) y \( {\vec T}_{2x} \) en la dirección x y componentes \( {\vec T}_{1y} \) y \( {\vec T}_{2y} \) en la dirección y.
\[
\begin{gather}
{\vec T}_1+{\vec T}_2+\vec P=0 \\[5pt]
{\vec T}_{1x}+{\vec T}_{1y}-{\vec T}_{2x}+{\vec T}_{2y}-\vec P=0 \tag{II}
\end{gather}
\]
- Dirección x:
\[
T_{1x}=T_1\operatorname{sen}15° \tag{III}
\]
\[
T_{2x}=T_2\operatorname{sen}15° \tag{IV}
\]
Observación: a diferencia de lo que usualmente se hace, donde el ángulo se mide respecto al
eje x y la componente en esa dirección es proporcional al coseno, aquí el ángulo se mide respecto
al eje y y la componente es proporcional al seno del ángulo.
- Dirección y:
\[
T_{1y}=T_1\cos 15° \tag{V}
\]
\[
T_{2y}=T_2\cos 15° \tag{VI}
\]
El peso está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{VII}
\end{gather}
\]
Sustituyendo las ecuaciones (III), (IV), (V), (VI) y (VII) en la ecuación (II) y separando las componentes
en las direcciones x e y.
- Dirección x:
\[
\begin{gather}
T_1\operatorname{sen}15°-T_2\operatorname{sen}15°=0
\end{gather}
\]
- Dirección y:
\[
\begin{gather}
T_1\cos 15°+T_2\cos 15°-mg=0
\end{gather}
\]
estas ecuaciones forman un sistema de dos ecuaciones con dos incógnitas (T1 y
T2)
\[
\begin{gather}
\left\{
\begin{array}{l}
T_1\operatorname{sen}15°-T_2\operatorname{sen}15°=0\\
T_1\cos 15°+T_2\cos 15°-P=0
\end{array}
\right.
\end{gather}
\]
aislando T1 en la primera ecuación del sistema
\[
\begin{gather}
T_1\operatorname{sen}15°-T_2\operatorname{sen}15°=0 \\[5pt]
T_1\cancel{\operatorname{sen}15°}=T_2\cancel{\operatorname{sen}15°} \\[5pt]
T_1=T_2 \tag{VIII}
\end{gather}
\]
sustituyendo el valor de (VIII) en la segunda ecuación del sistema
\[
\begin{gather}
T_2\cos 15°+T_2\cos 15°-mg=0 \\[5pt]
2 T_2\cos 15°=mg \\[5pt]
T_2=\frac{mg}{2\cos 15°}
\end{gather}
\]
sustituyendo los datos del problema
\[
\begin{gather}
T_2=\frac{100\times 9,8}{2\times 0,966} \\[5pt]
T_2=507,3
\end{gather}
\]
por la igualdad (VII)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_1=T_2=507,3\;\mathrm N}
\end{gather}
\]
Estudiando las fuerzas que actúan en el punto D.
Trazando una línea horizontal por el punto D, el ángulo entre esta línea y la cuerda \( \overline{AD} \) es de 45°, un ángulo alterno interno con el ángulo entre la cuerda \( \overline{AD} \) y el techo (Figura 3-A).
El ángulo entre la cuerda \( \overline{BD} \) y la línea horizontal es de 60°, un ángulo alterno interno con el ángulo entre la cuerda \( \overline{BD} \) y el techo.
Trazando una línea vertical por el punto D, el ángulo entre la cuerda \( \overline{DE} \) y esta línea es de 15°, siendo alterno interno con el ángulo encontrado en la primera parte del problema.
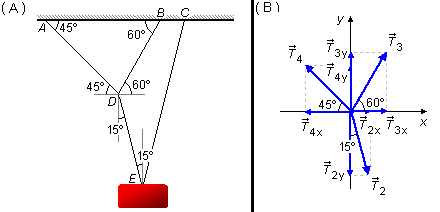
Dibujando las fuerzas en el punto D (Figura 3-B) en un sistema de coordenadas xy y descomponiendo las fuerzas, la tensión \( {\vec T}_2 \) ya fue determinada, tiene componentes \( {\vec T}_{2x} \) y \( {\vec T}_{2y} \)X. Las fuerzas de tensión \( {\vec T}_3 \) y \( {\vec T}_4 \) tienen componentes \( {\vec T}_{3x} \) y \( {\vec T}_{4x} \) en la dirección x y componentes \( {\vec T}_{3y} \) y \( {\vec T}_{4y} \) en la dirección y.
Como el sistema está en equilibrio, podemos aplicar la condición (I)
\[
\begin{gather}
{\vec T}_2+{\vec T}_3+{\vec T}_4=0 \\[5pt]
{\vec T}_{2x}-{\vec T}_{2y}+{\vec T}_{3x}+{\vec T}_{3y}-{\vec T}_{4x}+{\vec T}_{4y}=0 \tag{IX}
\end{gather}
\]
- Dirección x:
\[
T_{2x}=T_2\operatorname{sen}15° \tag{X}
\]
\[
T_{3x}=T_3\cos 60° \tag{XI}
\]
\[
T_{4x}=T_4\cos 45° \tag{XII}
\]
- Dirección y:
\[
T_{2y}=T_2\cos 15° \tag{XIII}
\]
\[
T_{3y}=T_3\operatorname{sen}60° \tag{XIV}
\]
\[
T_{4y}=T_4\operatorname{sen}45° \tag{XV}
\]
Sustituyendo las ecuaciones (X), (XI), (XII), (XIII), (XIV) y (XV) en la ecuación (IX) y separando las
componentes en las direcciones x e y
- Dirección x:
\[
\begin{gather}
T_2\operatorname{sen}15°+T_3\cos 60°-T_4\cos 45°=0\\[5pt]
\end{gather}
\]
- Dirección y:
\[
\begin{gather}
T_3\operatorname{sen}60°+T_4\operatorname{sen}45°-T_2\cos 15°=0
\end{gather}
\]
estas ecuaciones forman un sistema de dos ecuaciones con dos incógnitas (T3 y
T4)
Observación: T2 no es una incógnita, ya fue determinada anteriormente, por
lo que trasladamos los términos en T2 a la derecha de la igualdad.
\[
\begin{gather}
&\left\{
\begin{matrix}
T_2\operatorname{sen}15°+T_3\cos 60°-T_4\cos 45°=0\\
T_3\operatorname{sen}60°+T_4\operatorname{sen}45°-T_2\cos 15°=0
\end{matrix}
\right.\\[8pt]
&\left\{
\begin{matrix}
T_3\cos 60°-T_4\cos 45°=-T_2\operatorname{sen}15°\\
T_3\operatorname{sen}60°+T_4\operatorname{sen}45°=T_2\cos 15°
\end{matrix}
\right.
\end{gather}
\]
sumando las dos ecuaciones del sistema eliminamos el término en T4
\[
\begin{gather}
\frac{
\begin{matrix}
T_3\cos 60°-\cancel{T_4\cos 45°}=-T_2\operatorname{sen}15°\\
T_3\operatorname{sen}60°+\cancel{T_4\operatorname{sen}45°}=T_2\cos 15°
\end{matrix}}
{T_3(\cos 60°+\operatorname{sen}60°)+0=T_2(\cos 15°-\operatorname{sen}15°)}\\[5pt]
T_3=\frac{\cos 15°-\operatorname{sen}15°}{\cos 60°+\operatorname{sen}60°}\,T_2
\end{gather}
\]
Observación: recuerda que cos 45° es igual a sen 45°, por lo que estos términos se cancelan
cuando sumamos las dos ecuaciones, ya que tienen signos opuestos en las ecuaciones.
sustituyendo los valores dados en el problema y la tensión T2 determinada anteriormente
\[
\begin{gather}
T_3=\frac{0,966-0,258}{0,500+0,866}\times 507,3
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_3=262,9\;\mathrm N}
\end{gather}
\]
Aislando T4 en la segunda ecuación del sistema
\[
\begin{gather}
T_3\operatorname{sen}60°+T_4\operatorname{sen}45°=T_2\cos 15° \\[5pt]
T_4=\frac{T_2\cos 15°-T_3\operatorname{sen}60°}{\operatorname{sen}45°}
\end{gather}
\]
sustituyendo los valores dados en el problema y las tensiones T2 y T3
determinadas anteriormente
\[
\begin{gather}
T_4=\frac{507,3\times 0,966-262,9\times 0,866}{0,707}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_4=371,1\;\mathrm N}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .