Exercice Résolu sur les
publicité
Une balle roule sur une table horizontale d'une hauteur H, à une vitesse constante v0, sans frottement, jusqu'à tomber du bord. Calculer:
a) Le temps nécessaire pour que la balle touche le sol;
b) La distance horizontale, à partir du bord de la table, où la balle touche le sol;
c) L'équation de la trajectoire du mouvement;
d) La vitesse à laquelle la balle touche le sol.
Données du problème:
- Vitesse initiale de la balle sur la table: v0;
- Hauteur de la table: H.
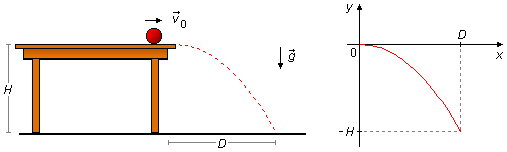
Nous choisissons un référentiel sur la table avec l'axe Ox pointant vers la droite et Oy vers le haut, l'accélération de la pesanteur est dirigée vers le bas et le point d'où la balle tombe de la table est à (x0, y0) = (0, 0), (Figure 1).
Solution
Le mouvement peut être décomposé dans les directions x et y. La vitesse initiale v0, avec laquelle la balle roule sur la table dans la direction x, sera la seule vitesse jusqu'au moment où la balle tombe du bord de la table, dans la direction y la vitesse initiale sera nulle
\[
\begin{gather}
v_{0 x} = v_0 \tag{I}\\[10pt]
v_{0 y} = 0 \tag{II}
\end{gather}
\]
En décomposant le mouvement, dans la direction x, il n'y a pas d'accélération agissant sur la balle,
elle est en Mouvement Rectiligne Uniforme et son mouvement est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_x=S_{0x}+v_xt}
\end{gather}
\]
comme dans le mouvement uniforme vx = v0x est constant, nous
pouvons remplacer vx par la valeur de (I) et S0x = 0
\[
\begin{gather}
S_x=0+v_0t\\[5pt]
S_x=v_0t \tag{III}
\end{gather}
\]
Dans la direction y, la balle est soumise à l'accélération de la gravité, donc elle est en chute libre
donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_y=S_{0y}+v_{0y}t-\frac{g}{2}t^2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_y=v_{0y}-gt}
\end{gather}
\]
en remplaçant v0y par la valeur donnée en (II) et
S0y = 0
\[
\begin{gather}
S_y=0+0\times t-\frac{g}{2}t^2\\[5pt]
S_y=-\frac{g}{2}t^2 \tag{IV}
\end{gather}
\]
\[
\begin{gather}
v_y=-gt \tag{V}
\end{gather}
\]
avec −g constant (le signe négatif indique que l'accélération de la gravité est opposée à
l'orientation de le référentiel).
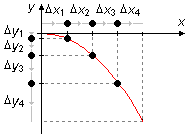
Dans la Figure 2, nous voyons que dans le mouvement le long de la direction x, pour des
intervalles de temps égaux, nous avons des intervalles d'espaces égaux
(Δx1 = Δx2 =
Δx3 = Δx4). Dans la direction y, au moment où la
balle tombe de la table, la vitesse vy commence à augmenter à partir de zéro sous
l'action de la gravité, pour des intervalles de temps égaux, nous avons des intervalles d'espaces de
plus en plus grands
(Δ1 < Δ2 < Δ3 <
Δ4).
a) L'intervalle de temps pour que la balle atteigne le sol sera obtenu à partir de l'équation (IV) avec la condition que au sol la hauteur est nulle, Sy = −H;
\[
\begin{gather}
-H--\frac{g}{2}t^2\\[5pt]
t^2=\frac{2H}{g}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=\sqrt{\frac{2H}{g}\;}}
\end{gather}
\]
b) L'intervalle de temps calculé ci-dessus, pour que la balle tombe jusqu'au sol, est également l'intervalle de temps qu'elle mettra pour aller de l'origine au point D le long de l'axe x, en remplaçant la réponse de l'élément précédent dans l'expression (III)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{D=v_0\sqrt{\frac{2H}{g}\;}}
\end{gather}
\]
c) Pour obtenir l'équation de la trajectoire (Figure 1), nous devons exprimer y en fonction de x, ou y = f(x), en utilisant les équations (III) et (IV) pour les mouvements en x et y. En isolant le temps dans l'expression (III)
\[
\begin{gather}
t=\frac{S_x}{v_0}
\end{gather}
\]
et en remplaçant cette valeur dans l'équation (IV)
\[
\begin{gather}
S_y=-\frac{g}{2}\left(\frac{S_x}{v_0}\right)^2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_y=-{\frac{g}{2v_0^2}S_x^2}}
\end{gather}
\]
En associant cela à une Équation du Second Degré de type
y = ax2+bx+c
\[
\begin{array}{c}
S_y & = & -{\dfrac{g}{2v_0^2}} & S_x^2 & + & 0 & S_x & + & 0\\
\downarrow & & \downarrow & \downarrow & & \downarrow & \downarrow & & \downarrow \\
y & = & a & x^2 & + & b & x & + & c
\end{array}
\]
nous voyons que nous avons obtenu une fonction du type Sy = f(Sx)
avec le coefficient a < 0, ce qui indique que la trajectoire est une parabole orientée vers le bas.
d) Lorsque la balle atteint le sol, sa vitesse a des composantes dans les directions x et y (Figure 3). La vitesse dans la direction x est donnée par l'expression (I) et la vitesse dans la direction y est obtenue à partir de l'expression (V) où le temps est remplacé par la valeur trouvée dans l'article (a)
\[
\begin{gather}
v_y=-g\sqrt{\frac{2H}{g}\;}\\[5pt]
v_y=-\sqrt{\frac{2Hg^{\cancel 2}}{\cancel g}\;}\\[5pt]
v_y=-\sqrt{2gH\;}
\end{gather}
\]
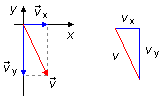
La vitesse de la balle est donnée par la somme vectorielle
\[
\begin{gather}
\vec v={\vec v}_x+{\vec v}_y
\end{gather}
\]
Le module est obtenu en appliquant le Théorème de Pythagore
\[
\begin{gather}
v^2=v_x^2+v_y^2\\[5pt]
v^2=v_0^2+\left(-\sqrt{2gH}\right)^2\\[5pt]
v^2=v_0^2+2gH
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=\sqrt{v_0^2+2gH\;}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .