Exercício Resolvido de Função de Onda
publicidade
No instante t = 0 uma partícula é representada pela seguinte função de onda
\[
\begin{gather}
\Psi (x,0)=
\left\{\begin{array}{l}
\;\dfrac{Ax}{a}\,,&\text{se}\;0\leqslant x\leqslant a\\
\;\dfrac{A(b-x)}{(b-a)}\,,&\text{se}\;a\leqslant x\leqslant b\\
\;\;0\,,&\text{nos demais pontos}
\end{array}
\right.
\end{gather}
\]
onde A, a e b são constantesa) Normalize Ψ (ou seja, determine A em função de a e b);
b) Esquematize o gráfico de Ψ(x, 0) como função de x;
c) Qual a posição mais provável da partícula em t = 0?
d) Qual é a probabilidade de encontrar a partícula à esquerda de a? Verifique seu resultado nos casos limites, b = a e b = 2a;
e) Qual o valor esperado de x?
Solução
a) O valor da constante A é calculado pela integral da normalização da função Ψ(x, 0)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\int_{{-\infty}}^{{\infty}}\left|\Psi (x,t)\right|^{\;2}\;dx=1}
\end{gather}
\]
A função Ψ(x, 0) dada no problema é uma Função Definida por Partes, para normalizar a
função devemos fazer a soma das integrais sobre cada um dos intervalos da função
\[
\begin{gather}
\int_{{0}}^{{a}}\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx=1 \tag{I}
\end{gather}
\]
Integral de
\( \displaystyle \int_{{0}}^{{a}}\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx \)
para x = a
temos u = b−a
para x = b
temos u = 0
\[
\begin{align}
\int_{{0}}^{{a}}\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx & \Rightarrow\frac{|A|^{\;2}}{a^{2}}\int_{{0}}^{{a}}x^{2}\;dx+\frac{|A|^{2}}{(b-a)^{2}}\int_{{a}}^{{b}}(b-x)^{2}\;dx\Rightarrow\\[5pt]
& \Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\left.\frac{x^{3}}{3}\right|_{\;0}^{\;a}\right)+\frac{|A|^{2}}{(b-a)^{2}}\int_{{a}}^{{b}}(b-x)^{2}\;dx
\end{align}
\]
Fazendo a mudança de variável na segunda integral
\[
\begin{array}{l}
u=b-x\\[5pt]
\dfrac{du}{dx}=-1\Rightarrow dx=-du
\end{array}
\]
fazendo a mudança nos extremos de integração
para x = a
temos u = b−a
para x = b
temos u = 0
\[
\begin{align}
\int_{{0}}^{{a}} & \left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx\Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\frac{a^{3}}{3}-\frac{0^{3}}{3}\right)+\frac{|A|^{2}}{(b-a)^{2}}\int_{{b-a}}^{{0}}-u^{2}\;du\Rightarrow\\[5pt]
& \Rightarrow|A|^{2}\left\{\frac{1}{a^{2}}\frac{a^{3}}{3}+\frac{1}{(b-a)^{2}}\int_{{b-a}}^{{0}}-u^{2}\;du\right\}\Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\int_{{0}}^{{b-a}}u^{2}\;du\right\}\Rightarrow\\[5pt]
& \Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\left(\left.\frac{u^{3}}{3}\right|_{0}^{b-a}\right)\right\}\Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\left(\frac{(b-a)^{3}}{3}-\frac{0^{3}}{3}\right)\right\}\Rightarrow\\[5pt]
& \Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\frac{(b-a)^{3}}{3}\right\}\Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{b-a}{3}\right\}\Rightarrow|A|^{2}\frac{b}{3} \tag{II}
\end{align}
\]
Substituindo a expressão (II) na equação (I)
\[
\begin{gather}
|A|^{2}\frac{b}{3}=1\\[5pt]
|A|^{2}=\frac{3}{b}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{A=\sqrt{\frac{3}{b}}}
\end{gather}
\]
b) Esquema da função Ψ(x, 0) (Figura 1)
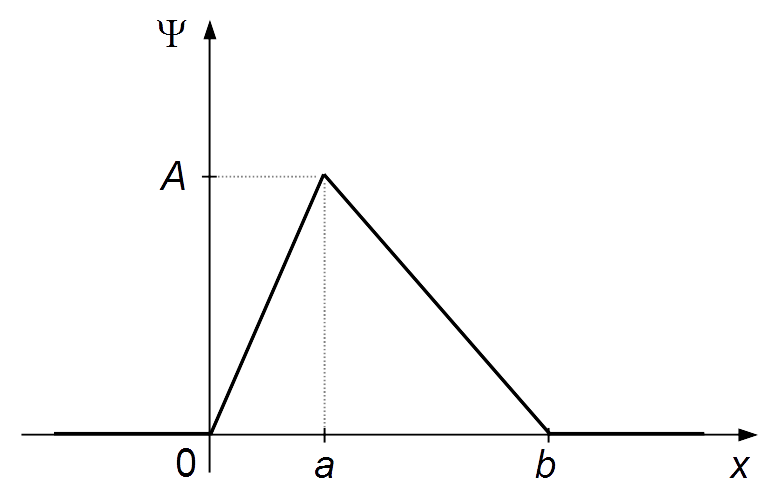
c) Analisando o gráfico do item anterior vemos que a posição mais provável é
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x=a}
\end{gather}
\]
d) A probabilidade de encontrar a partícula em uma posição é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=\Psi^{\Large *}(x,t)\Psi(x,t)}
\end{gather}
\]
para encontrar a partícula à esquerda do ponto a calculamos a integral de 0 até a
\[
\begin{gather}
P=\int_{{0}}^{{a}}\left|\frac{Ax}{a}\right|^{\;2}\;dx
\end{gather}
\]
Integral de
\( \displaystyle \int_{{0}}^{{a}}\left|\frac{Ax}{a}\right|^{\;2}\;dx \)
\[
\begin{align}
\int_{{0}}^{{a}}\left|\frac{Ax}{a}\right|^{\;2}\;dx & \Rightarrow \int_{{0}}^{{a}}{\frac{|A|^{\;2}x^{2}}{a^{2}}\;dx}\Rightarrow\frac{|A|^{\;2}}{a^{\;2}}\int_{{0}}^{{a}}{x^{2}\;dx}\Rightarrow\\[5pt]
& \Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\left.\frac{x^{3}}{3}\right|_{0}^{a}\right)\Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\frac{a^{3}}{3}-\frac{0^{3}}{3}\right)\Rightarrow\\[5pt]
& \Rightarrow\frac{|A|^{\;2}}{a^{2}}\frac{a^{3}}{3}\Rightarrow|A|^{\;2}\frac{a}{3}\Rightarrow \frac{3}{b}\frac{a}{3}\Rightarrow\frac{a}{b}
\end{align}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=\frac{a}{b}}
\end{gather}
\]
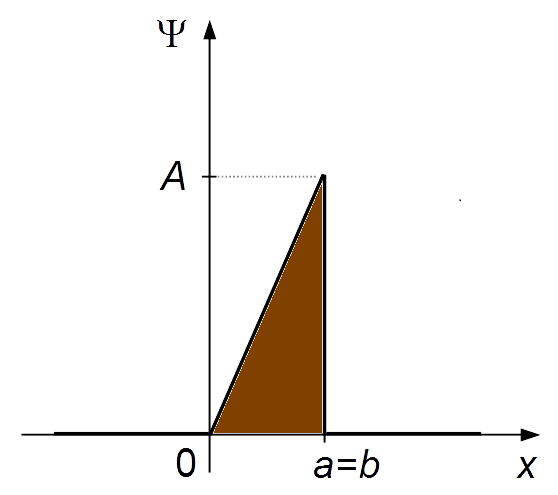
- 1.º caso: b = a
\[
\begin{gather}
P=\frac{a}{a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=1}
\end{gather}
\]
Observação: Neste caso o ponto b coincide com o ponto a, só existe o lado
esquerdo da função de onda. A probabilidade de encontrar a partícula à esquerda é
\( P=1=100 \% \)
(Figura 2).
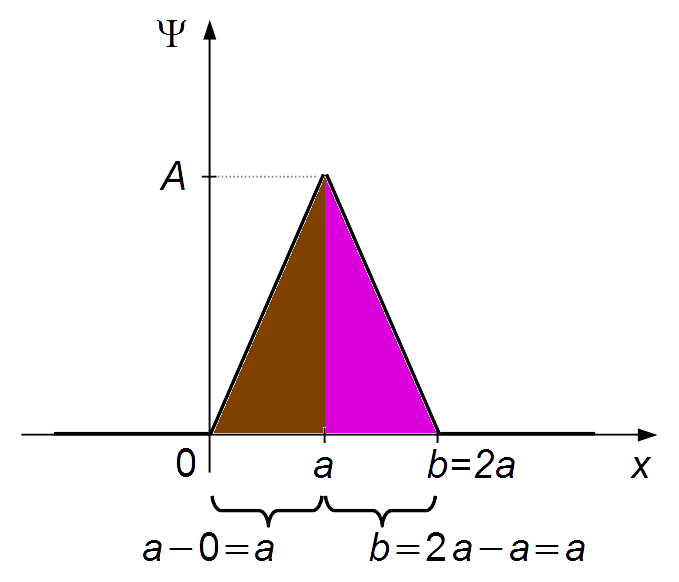
- 2.º caso: b = 2a
\[
\begin{gather}
P=\frac{a}{2a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=\frac{1}{2}}
\end{gather}
\]
Observação: Neste caso a distância da origem ao ponto a é igual à distância do
ponto a ao ponto b, as áreas à direita e à esquerda do ponto a são iguais.
A probabilidade de encontrar a partícula à esquerda (ou à direita) é
\( P=\frac{1}{2}=50\text{%} \)
(Figura 3).
e) O valor esperado de x é calculado pela integral
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\langle x\rangle =\int_{{-\infty}}^{{\infty}}x\left|\Psi(x,t)\right|^{\;2}\;dx}
\end{gather}
\]
\[
\begin{gather}
\langle x\rangle =\int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx
\end{gather}
\]
Integral de
\( \displaystyle \int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx \)
\[ \displaystyle \int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx \]
\[
\begin{align}
\int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx & +\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx\Rightarrow\frac{\left|A\right|^{2}}{a^{2}}\int_{{0}}^{{a}}xx^{2}\;dx+\frac{\left|A\right|^{2}}{(b-a)^{2}}\int_{{a}}^{{b}}x(b-x)^{2}\;dx\Rightarrow \\[5pt]
& \Rightarrow\left|A\right|^{2}\left\{\frac{1}{a^{2}}\int_{{0}}^{{a}}x^{3}\;dx+\frac{1}{(b-a)^{2}}\int_{{a}}^{{b}}x(b^{2}-2bx+x^{2})\;dx\right\}\Rightarrow \\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{1}{a^{2}}\left(\left.\frac{x^{4}}{4}\right|_{\;0}^{\;a}\right)+\frac{1}{(b-a)^{2}}\int_{{a}}^{{b}}(b^{2}x-2bx^{2}+x^{3})\;dx\right\}\Rightarrow \\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{1}{a^{2}}\left(\frac{a^{4}}{4}-\frac{0^{4}}{4}\right)+\frac{1}{(b-a)^{2}}\left[\left.\left(b^{2}\frac{x^{2}}{2}-2b\frac{x^{3}}{3}+\frac{x^{4}}{4}\right)\right|_{\;a}^{\;b}\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{1}{a^{2}}\frac{a^{4}}{4}+\frac{1}{(b-a)^{2}}\left[\left(b^{2}\frac{b^{2}}{2}-2b\frac{b^{3}}{3}+\frac{b^{4}}{4}\right)-\left(b^{2}\frac{a^{2}}{2}-2b\frac{a^{3}}{3}+\frac{a^{4}}{4}\right)\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{a^{2}}{4}+\frac{1}{(b-a)^{2}}\left[\frac{b^{4}}{2}-\frac{2b^{4}}{3}+\frac{b^{4}}{4}-\frac{a^{2}b^{2}}{2}+\frac{2a^{3}b}{3}-\frac{a^{4}}{4}\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{a^{2}}{4}+\frac{1}{(b-a)^{2}}\left[\frac{6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{12}\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{4b(b-a)^{2}}\left\{a^{2}(b-a)^{2}+\frac{6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{3}\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{4b(b-a)^{2}}\left\{\frac{3a^{2}(b^{2}-2ab+a^{2})+6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{3}\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{4b(b-a)^{2}}\left\{\frac{3a^{2}b^{2}-6a^{3}b+3a^{4}+6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{3}\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{\left(b^{4}-3a^{2}b^{2}+2a^{3}b\right)}{4b(b-a)^{2}}\Rightarrow\frac{b^{3}-3a^{2}b^{}+2a^{3}}{4(b-a)^{2}}
\end{align}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\langle x\rangle =\frac{2a+b}{4}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .