Solved Problem on Wave Function
advertisement
At time t = 0, a particle is represented by the following wave function
\[
\begin{gather}
\Psi (x,0)=
\left\{\begin{array}{l}
\;\dfrac{Ax}{a}\,,&\text{if}\;0\leqslant x\leqslant a\\
\;\dfrac{A(b-x)}{(b-a)}\,,&\text{if}\;a\leqslant x\leqslant b\\
\;\;0\,,&\text{otherwise}
\end{array}
\right.
\end{gather}
\]
where A, a, and b are constantsa) Normalize Ψ (that is, determine A in terms of a and b);
b) Sketch Ψ(x, 0) as a function of x;
c) What is the particle most likely to be found of at t = 0?
d) What is the probability of finding the particle to the left of a? Check your result in the limiting cases, b = a and b = 2a;
e) What is the expectation value of x?
Solution
a) The value of the constant A is calculated by the integral of the normalization of the function Ψ(x, 0)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\int_{{-\infty}}^{{\infty}}\left|\Psi (x,t)\right|^{\;2}\;dx=1}
\end{gather}
\]
The function Ψ(x, 0) given in the problem is a Piecewise Function to normalize the
function. we add the integrals over each of the intervals of the function
\[
\begin{gather}
\int_{{0}}^{{a}}\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx=1 \tag{I}
\end{gather}
\]
Integral of
\( \displaystyle \int_{{0}}^{{a}}\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx \)
for x = a
we have u = b−a
for x = b
we have u = 0
\[
\begin{align}
\int_{{0}}^{{a}}\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx & \Rightarrow\frac{|A|^{\;2}}{a^{2}}\int_{{0}}^{{a}}x^{2}\;dx+\frac{|A|^{2}}{(b-a)^{2}}\int_{{a}}^{{b}}(b-x)^{2}\;dx\Rightarrow\\[5pt]
& \Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\left.\frac{x^{3}}{3}\right|_{\;0}^{\;a}\right)+\frac{|A|^{2}}{(b-a)^{2}}\int_{{a}}^{{b}}(b-x)^{2}\;dx
\end{align}
\]
Changing of variable in the second integral
\[
\begin{array}{l}
u=b-x\\[5pt]
\dfrac{du}{dx}=-1\Rightarrow dx=-du
\end{array}
\]
changing the limits of integration
for x = a
we have u = b−a
for x = b
we have u = 0
\[
\begin{align}
\int_{{0}}^{{a}} & \left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx\Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\frac{a^{3}}{3}-\frac{0^{3}}{3}\right)+\frac{|A|^{2}}{(b-a)^{2}}\int_{{b-a}}^{{0}}-u^{2}\;du\Rightarrow\\[5pt]
& \Rightarrow|A|^{2}\left\{\frac{1}{a^{2}}\frac{a^{3}}{3}+\frac{1}{(b-a)^{2}}\int_{{b-a}}^{{0}}-u^{2}\;du\right\}\Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\int_{{0}}^{{b-a}}u^{2}\;du\right\}\Rightarrow\\[5pt]
& \Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\left(\left.\frac{u^{3}}{3}\right|_{0}^{b-a}\right)\right\}\Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\left(\frac{(b-a)^{3}}{3}-\frac{0^{3}}{3}\right)\right\}\Rightarrow\\[5pt]
& \Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{1}{(b-a)^{2}}\frac{(b-a)^{3}}{3}\right\}\Rightarrow|A|^{2}\left\{\frac{a}{3}+\frac{b-a}{3}\right\}\Rightarrow|A|^{2}\frac{b}{3} \tag{II}
\end{align}
\]
Substituting expression (II) into equation (I)
\[
\begin{gather}
|A|^{2}\frac{b}{3}=1\\[5pt]
|A|^{2}=\frac{3}{b}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{A=\sqrt{\frac{3}{b}}}
\end{gather}
\]
b) Sketch of the function Ψ(x, 0) (Figure 1)
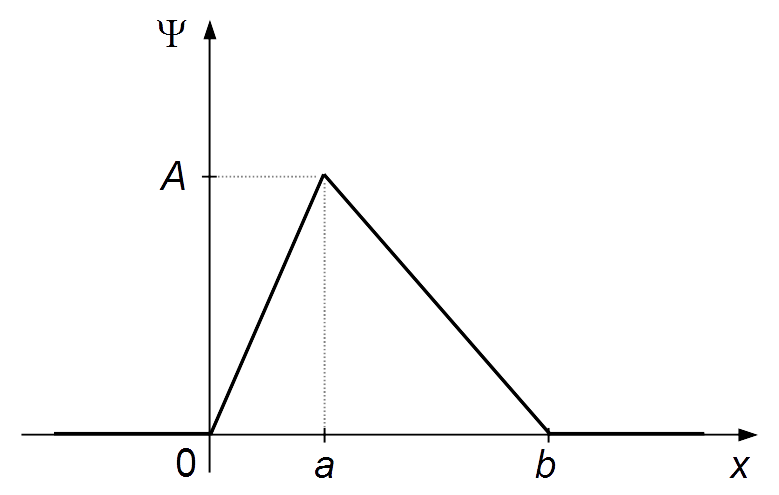
c) Analyzing the graph of the previous item, we see that the most likely position is
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x=a}
\end{gather}
\]
d) The probability of finding the particle in one position is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=\Psi^{\Large *}(x,t)\Psi(x,t)}
\end{gather}
\]
to find the particle to the left of point a, we calculate the integral from 0 to a
\[
\begin{gather}
P=\int_{{0}}^{{a}}\left|\frac{Ax}{a}\right|^{\;2}\;dx
\end{gather}
\]
Integral of
\( \displaystyle \int_{{0}}^{{a}}\left|\frac{Ax}{a}\right|^{\;2}\;dx \)
\[
\begin{align}
\int_{{0}}^{{a}}\left|\frac{Ax}{a}\right|^{\;2}\;dx & \Rightarrow \int_{{0}}^{{a}}{\frac{|A|^{\;2}x^{2}}{a^{2}}\;dx}\Rightarrow\frac{|A|^{\;2}}{a^{\;2}}\int_{{0}}^{{a}}{x^{2}\;dx}\Rightarrow\\[5pt]
& \Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\left.\frac{x^{3}}{3}\right|_{0}^{a}\right)\Rightarrow\frac{|A|^{\;2}}{a^{2}}\left(\frac{a^{3}}{3}-\frac{0^{3}}{3}\right)\Rightarrow\\[5pt]
& \Rightarrow\frac{|A|^{\;2}}{a^{2}}\frac{a^{3}}{3}\Rightarrow|A|^{\;2}\frac{a}{3}\Rightarrow \frac{3}{b}\frac{a}{3}\Rightarrow\frac{a}{b}
\end{align}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=\frac{a}{b}}
\end{gather}
\]
- 1st case: b = a
\[
\begin{gather}
P=\frac{a}{a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=1}
\end{gather}
\]
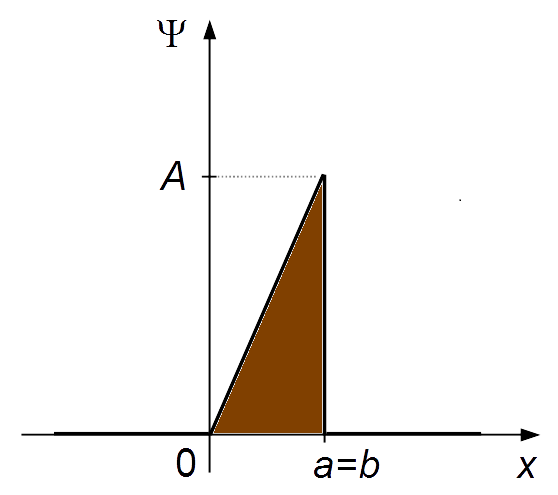
Note: In this case, point b coincides with point a, and there is only the
left side of the wave function. The probability of finding the particle on the left is
\( P=1=100 \% \)
(Figure 2).
- 2nd case: b = 2a
\[
\begin{gather}
P=\frac{a}{2a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=\frac{1}{2}}
\end{gather}
\]
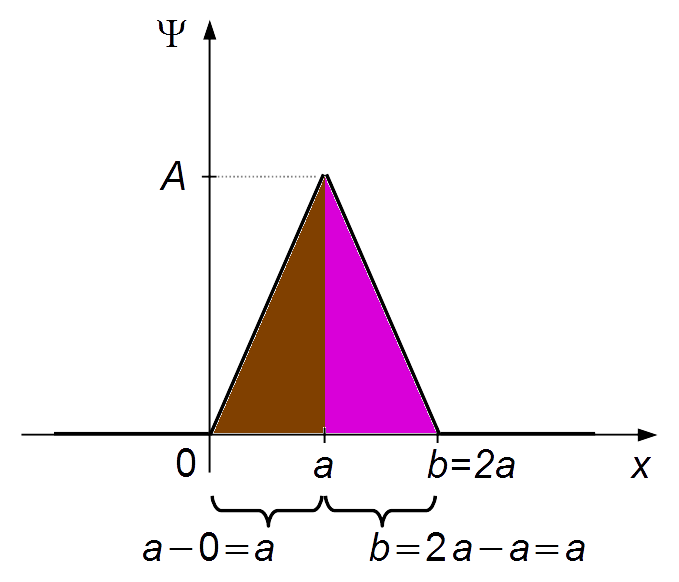
Note: In this case, the distance from the origin to point a is equal to the
distance from point a to point b, and the areas to the right and left of point a
are equal. The probability of finding the particle on the left (or on the right) is
\( P=\frac{1}{2}=50\text{%} \)
(Figure 3).
e) The expectation value of x is calculated by the integral
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\langle x\rangle =\int_{{-\infty}}^{{\infty}}x\left|\Psi(x,t)\right|^{\;2}\;dx}
\end{gather}
\]
\[
\begin{gather}
\langle x\rangle =\int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx
\end{gather}
\]
Integral of
\( \displaystyle \int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx \)
\[ \displaystyle \int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx+\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx \]
\[
\begin{align}
\int_{{0}}^{{a}}x\left|\frac{A}{a}x\right|^{2}\;dx & +\int_{{a}}^{{b}}x\left|\frac{A(b-x)}{(b-a)}\right|^{2}\;dx\Rightarrow\frac{\left|A\right|^{2}}{a^{2}}\int_{{0}}^{{a}}xx^{2}\;dx+\frac{\left|A\right|^{2}}{(b-a)^{2}}\int_{{a}}^{{b}}x(b-x)^{2}\;dx\Rightarrow \\[5pt]
& \Rightarrow\left|A\right|^{2}\left\{\frac{1}{a^{2}}\int_{{0}}^{{a}}x^{3}\;dx+\frac{1}{(b-a)^{2}}\int_{{a}}^{{b}}x(b^{2}-2bx+x^{2})\;dx\right\}\Rightarrow \\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{1}{a^{2}}\left(\left.\frac{x^{4}}{4}\right|_{\;0}^{\;a}\right)+\frac{1}{(b-a)^{2}}\int_{{a}}^{{b}}(b^{2}x-2bx^{2}+x^{3})\;dx\right\}\Rightarrow \\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{1}{a^{2}}\left(\frac{a^{4}}{4}-\frac{0^{4}}{4}\right)+\frac{1}{(b-a)^{2}}\left[\left.\left(b^{2}\frac{x^{2}}{2}-2b\frac{x^{3}}{3}+\frac{x^{4}}{4}\right)\right|_{\;a}^{\;b}\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{1}{a^{2}}\frac{a^{4}}{4}+\frac{1}{(b-a)^{2}}\left[\left(b^{2}\frac{b^{2}}{2}-2b\frac{b^{3}}{3}+\frac{b^{4}}{4}\right)-\left(b^{2}\frac{a^{2}}{2}-2b\frac{a^{3}}{3}+\frac{a^{4}}{4}\right)\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{a^{2}}{4}+\frac{1}{(b-a)^{2}}\left[\frac{b^{4}}{2}-\frac{2b^{4}}{3}+\frac{b^{4}}{4}-\frac{a^{2}b^{2}}{2}+\frac{2a^{3}b}{3}-\frac{a^{4}}{4}\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{b}\left\{\frac{a^{2}}{4}+\frac{1}{(b-a)^{2}}\left[\frac{6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{12}\right]\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{4b(b-a)^{2}}\left\{a^{2}(b-a)^{2}+\frac{6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{3}\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{4b(b-a)^{2}}\left\{\frac{3a^{2}(b^{2}-2ab+a^{2})+6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{3}\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{3}{4b(b-a)^{2}}\left\{\frac{3a^{2}b^{2}-6a^{3}b+3a^{4}+6b^{4}-8b^{4}+3b^{4}-6a^{2}b^{2}+8a^{3}b-3a^{4}}{3}\right\}\Rightarrow\\[5pt]
& \Rightarrow\frac{\left(b^{4}-3a^{2}b^{2}+2a^{3}b\right)}{4b(b-a)^{2}}\Rightarrow\frac{b^{3}-3a^{2}b^{}+2a^{3}}{4(b-a)^{2}}
\end{align}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\langle x\rangle =\frac{2a+b}{4}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .