Exercício Resolvido de Contornos
Português
English
publicidade
\( \mathsf{e)}\;\; \displaystyle z=t+i\sqrt{1-t^{2}\;}\qquad ,\qquad -1\leqslant t\leqslant 1 \)
A função z é uma função paramétrica do tipo
\[ \bbox[#99CCFF,10px]
{z(t)=x(t)+iy(t)}
\]
Identificando as funções x(t) e y(t)
\[
\begin{align}
& x(t)=t \tag{I}\\[10pt]
& y(t)=\sqrt{1-t^{2}\;} \tag{II}
\end{align}
\]
substituindo a expressão (I) na expressão (II)
\[
y=\sqrt{1-x^{2}\;}
\]
elevando ao quadrado ambos os lados da igualdade
\[
\begin{gather}
y^{2}=\left(\sqrt{1-x^{2}\;}\right)^{2}\\
y^{2}=1-x^{2}\\
y^{2}+x^{2}=1
\end{gather}
\]
Para t = −1, temos x = −1 e
\( y=\sqrt{1-(-1)^{2}\;}=0 \),
para t = 0, temos x = 0 e
\( y=\sqrt{1-0^{2}\;}=1 \),
para t = 1, temos x = 1 e
\( y=\sqrt{1-1^{2}\;}=0 \).
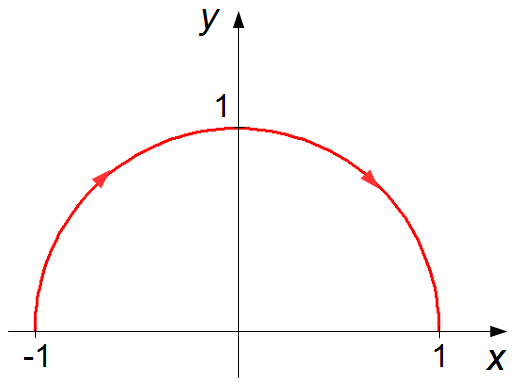
A função z(t) representa uma semicircunferência acima do eixo-x e orientada de −1 para 1, (Gráfico 1).
publicidade
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .