Exercício Resolvido de Momento de Inércia
publicidade
Demonstre o Teorema dos Eixos Perpendiculares.
Esquema do problema:
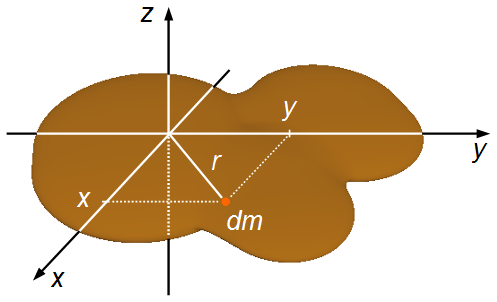
Na Figura 1, dm é um elemento de massa do corpo, r é a distância do elemento de massa até
um eixo perpendicular ao corpo (não necessariamente passando pelo Centro de Massa).
Solução
Na Figura 1 o eixo-z é perpendicular ao plano que contém o corpo, x e y são eixos que estão no mesmo plano do corpo.
O momento de inércia em relação ao eixo-z é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I_{z}=\int r^{2}\;dm} \tag{I}
\end{gather}
\]
Escrevendo o momento de inércia para os dois eixos contidos no mesmo plano do corpo
\[
\begin{gather}
I_{x}=\int x^{2}\;dm \tag{II-a}
\end{gather}
\]
\[
\begin{gather}
I_{y}=\int y^{2}\;dm \tag{II-b}
\end{gather}
\]
Aplicando o Teorema de Pitágoras (Figura 1)
\[
\begin{gather}
r^{2}=x^{2}+y^{2} \tag{III}
\end{gather}
\]
substituindo a expressão (II) na expressão (I)
\[
\begin{gather}
I=\int \left(x^{2}+y^{2}\right)\;dm \tag{IV}
\end{gather}
\]
a integral da soma de funções é igual soma das integrais
\[
\begin{gather}
I=\int x^{2}\;dm+\int y^{2}\;dm \tag{V}
\end{gather}
\]
substituindo as expressões (II-a) e (II-b) na expressão (V)
\[ \bbox[#FFCCCC,10px]
{I=I_{x}+I_{y}} \tag{Q.E.D.}
\]
Observação: Q.E.D é a abreviação da expressão em latim Quod Erat Demonstrandum que
significa Como Queríamos Demonstrar.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .