Exercício Resolvido de Força Elétrica e Campo Elétrico
Português
English
publicidade
Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento L.
Determinar o vetor campo elétrico nos pontos situados sobre a reta perpendicular ao fio e que passa pelo
meio do fio.
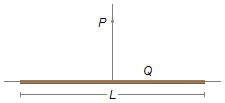
Dados do problema:
- Comprimento do fio: L;
- Carga do fio: Q.
O vetor posição r vai de um elemento de carga dq do fio até o ponto P onde se deseja calcular o campo elétrico, o vetor rq localiza o elemento de carga em relação à origem do referencial e o vetor rp localiza o ponto P (Figura1-A).
\[
\mathbf{r}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\]
Pela geometria do problema devemos escolher coordenadas cartesianas, o vetor rq só possui componente na direção i, é escrito como \( {\mathbf{r}}_{q}=x\;\mathbf{i} \) e o vetor rp só possui componente na direção j, é escrito como \( {\mathbf{r}}_{p}=y\;\mathbf{j} \) (Figura 1-B), então o vetor posição será
\[
\begin{gather}
\mathbf{r}=y\;\mathbf{j}-x\;\mathbf{i} \tag{I}
\end{gather}
\]
Da expressão (I) o módulo do vetor posição r será
\[
\begin{gather}
r^{2}=(-x)^{2}+y^{2}\\
r=\left(x^{2}+y^{2}\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
Solução
O vetor campo elétrico do fio é dado por
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{III}
\end{gather}
\]
Da expressão da densidade linear de carga λ obtemos o elemento de carga dq
\[ \bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\]
\[
\begin{gather}
dq=\lambda \;ds \tag{IV}
\end{gather}
\]
onde ds é um elemento de comprimento do fio
\[
\begin{gather}
ds=dx \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (IV)
\[
\begin{gather}
dq=\lambda \;dx \tag{VI}
\end{gather}
\]
Substituindo as expressões (I), (II) e (VI) na expressão (III)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int {\frac{\lambda\;dx}{\left[\left(x^{2}+y^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda\;dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right) \tag{VII}
\end{gather}
\]
A densidade de carga λ é constante ela pode “sair” da integral
\[
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int{\frac{dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)
\]
Como o ponto P está sobre a reta que divide o fio ao meio, a integral será feita sobre todos os
elementos de comprimento dx indo de
\( -{\frac{L}{2}} \)
até
\( \frac{L}{2} \)
(Figura 2)
\[
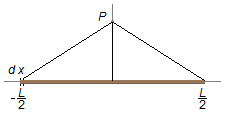
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)
\]
colocando y em evidência no numerador e y2 no denominador
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{\left[y^{2}\left(1+\dfrac{x^{2}}{y^{2}}\right)\right]^{\frac{3}{2}}}}y\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{\left(y^{2}\right)^{\frac{3}{2}}\left[1+\left(\dfrac{x}{y}\right)^{2}\right]^{\frac{3}{2}}}}y\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{\cancelto{2}{3}}\left[1+\left(\dfrac{x}{y}\right)^{2}\;\right]^{\frac{3}{2}}}}\cancel{y}\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\dfrac{x}{y}\right)^{2}\right]^{\frac{3}{2}}}}\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right) \tag{VIII}
\end{gather}
\]
Considerando o ângulo θ medido entre o eixo-y e a distância r do elemento de carga
dq ao ponto P, a tangente deste ângulo será (Figura 3)
\[
\begin{gather}
\operatorname{tg}\theta =\frac{x}{y} \\
x=y\operatorname{tg}\theta \tag{IX}
\end{gather}
\]
substituindo a expressão (IX) na expressão (VIII)
\[
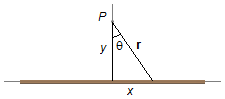
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\dfrac{\cancel{y}\operatorname{tg}\theta}{\cancel{y}}\right)^{2}\right]^{\frac{3}{2}}}}\left(-{\frac{\cancel{y}\operatorname{tg}\theta}{\cancel{y}}}\;\mathbf{i}+\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\operatorname{tg}\theta\right)^{2}\right]^{\frac{3}{2}}}}\left(-\operatorname{tg}\theta\;\mathbf{i}+\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{\mathit{dx}}{y^{2}\left(1+\operatorname{tg}^{2}\theta\right)^{\frac{3}{2}}}}\left(-\operatorname{tg}\theta\;\mathbf{i}+\;\mathbf{j}\right) \tag{X}
\end{gather}
\]
A partir da expressão (IX) obtemos o elemento de comprimento dx em relação ao elemento de arco
dθ.
Derivada de
\( x=y\operatorname{tg}\theta \)
\[
\frac{dx}{d\theta}=y\frac{d}{d\theta}\left(\operatorname{tg}\theta \right)
\]
reescrevendo
\( \operatorname{tg}\theta=\dfrac{\operatorname{sen}\theta}{\cos \theta} \),
temos a derivada de um quociente de funções dada pela fórmula
\[
\left(\frac{u}{v}\right)^{\Large '}=\frac{u'v-u\;v'}{v^{2}}
\]
\[
\begin{align}
\frac{d}{d\theta}\left(\operatorname{tg}\theta \right)=\frac{d}{d\theta}\left(\frac{\operatorname{sen}\theta}{\cos \theta}\right) &=\frac{\cos\theta \cos \theta-\operatorname{sen}\theta (-\sin\theta)}{(\cos \theta)^{2}}=\\
&=\frac{\cos ^{2}\theta+\operatorname{sen}^{2}\theta}{\cos ^{2}\theta}=\frac{1}{\cos^{2}\theta}
\end{align}
\]
\[
\begin{gather}
\frac{dx}{d\theta}=y\frac{1}{\cos ^{2}\theta}
\end{gather}
\]
Observação: Via de regra os livros de
Cálculo Integral e Diferencial apresentam a derivada da tangente na forma
\( \left(\operatorname{tg}\theta \right)^{'}=\sec^{2}\theta \),
onde
\( \sec\theta=\dfrac{1}{\cos \theta} \),
mas aqui por razões de simplificações posteriores vamos deixar a derivada na
forma mostrada acima.
\[
\begin{gather}
dx=y\frac{1}{\cos ^{2}\theta}\;d\theta \tag{XI}
\end{gather}
\]
substituindo a definição da tangente e a expressão (XI) na expressão (X)
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{1}{y^{\cancel{2}}\left[1+\left(\dfrac{\operatorname{sen}\theta}{\cos \theta}\;\right)^{2}\;\right]^{\frac{3}{2}}}}\cancel{y}\;\frac{d\theta}{\cos^{2}\theta}\;\left(\;-\frac{\operatorname{sen}\theta}{\cos \theta}\;\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{1}{y\left[1+\left(\dfrac{\operatorname{sen}\theta}{\cos \theta}\;\right)^{2}\;\right]^{\frac{3}{2}}}}\;\frac{d\theta}{\cos^{2}\theta}\;\left(\;-\frac{\operatorname{sen}\theta}{\cos \theta}\;\mathbf{i}+\;\mathbf{j}\;\right)
\end{gather}
\]
Os extremos de integração para a variável θ devem variar de
−θm, o valor máximo medido no sentido horário, quando
x vale
\( -{\frac{L}{2}} \),
até θm o valor máximo medido no sentido anti-horário,
quando x vale
\( {\frac{L}{2}} \)
(Figura 4).
\[
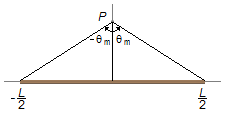
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi\epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\left(1+\dfrac{\operatorname{sen}^{2}\theta}{\cos^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\operatorname{sen}\theta}{\cos\theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\left(\dfrac{\cos ^{2}+\operatorname{sen}^{2}\theta}{\cos ^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos^{2}\theta}\;\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\left(\dfrac{1}{\cos ^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\dfrac{1}{\left(\cos ^{2}\theta\right)^{\frac{3}{2}}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}\;}\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\dfrac{1}{\cos ^{\cancel{3}}\theta}}}\;\frac{d\theta}{\cancel{\cos^{2}\theta}}\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\dfrac{1}{\cos \theta}}}\;d\theta\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{\cos\theta}{y}}\;d\theta \left(-{\frac{\operatorname{sen}\theta}{\cos\theta}}\;\mathbf{i}+\;\mathbf{j}\right)
\end{gather}
\]
Como y é constante ele pode “sair” da integral e a integral da soma é igual à soma das integrais
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0} y}\left(-\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta\frac{\operatorname{sen}\theta}{\cos \theta}\;d\theta\;\mathbf{i}+\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos\theta \;d\theta\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}\left(\underbrace{-{\int_{{-\theta_{m}}}^{{\theta_{m}}}\operatorname{sen}\theta \;d\theta\;\mathbf{i}}}_{0}+\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta\;\mathbf{j}\right)
\end{gather}
\]
Integral de \( \displaystyle \int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta \)
1.º método
Como a função cosseno é uma função par, f(x) = f(−x), podemos integrar sobre metade do intervalo, de 0 a θm, e multiplicar a integral por 2
Podemos integrar sobre todo intervalo, de −θm a θm
1.º método
Como a função cosseno é uma função par, f(x) = f(−x), podemos integrar sobre metade do intervalo, de 0 a θm, e multiplicar a integral por 2
\[
\begin{align}
2\int_{0}^{{\theta_{m}}}\cos \theta \;d\theta &=2\left.\operatorname{sen}\theta \right|_{\;0}^{\;\theta_{m}}=2(\operatorname{sen}\theta_{m}-\operatorname{sen}0)=\\
&=2(\operatorname{sen}\theta_{m}-0)=2\operatorname{sen}\theta_{m}
\end{align}
\]
2.º método
Podemos integrar sobre todo intervalo, de −θm a θm
\[
\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta=\left.\operatorname{sen}\theta \;\right|_{\;-\theta_{m}}^{\;\theta_{m}}=\operatorname{sen}\theta_{m}-\operatorname{sen}(-\theta_{m})
\]
como seno é uma função ímpar, f(−x) = −f(x), temos
\( \operatorname{sen}(-\theta_{m})=-\operatorname{sen}(\theta_{m}) \)
\[
\begin{align}
\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta &=\operatorname{sen}\theta_{m}-(-\operatorname{sen}\theta_{m})=\\
&=\operatorname{sen}\theta_{m}+\operatorname{sen}(\theta_{m})=2\operatorname{sen}\theta_{m}
\end{align}
\]
Integral de \( \displaystyle \int_{{-\theta_{m}}}^{{\theta_{m}}}\operatorname{sen}\theta \;d\theta \)
1.º método
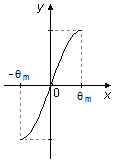
Figura 5
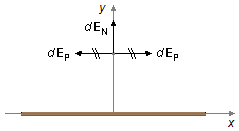Figura 6
1.º método
\[
\int_{{-\theta_{m}}}^{{\theta_{m}}}\operatorname{sen}\theta \;d\theta=-\left.\cos \theta \;\right|_{\;-\theta_{m}}^{\;\theta_{m}}=-\left[\cos \theta_{m}-\cos (-\theta_{m})\right]
\]
como cosseno é uma função par, f(x) = f(−x), temos
\( \cos (\theta_{m})=\cos (-\theta_{m}) \)
\[
\int_{{-\theta_{m}}}^{{\theta_{m}}}\operatorname{sen}\theta\;d\theta =-(\cos \theta_{m}-\cos \theta_{m})=0
\]
2.º método
O gráfico do seno entre −θm e 0 possui uma área “negativa” abaixo do eixo-x, e entre 0 e θm uma área “positiva” acima do eixo-x, estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero. na direção i (Figura 5).
O gráfico do seno entre −θm e 0 possui uma área “negativa” abaixo do eixo-x, e entre 0 e θm uma área “positiva” acima do eixo-x, estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero. na direção i (Figura 5).
Figura 5
Observação: A integral na direção i, que é nula, representa o cálculo matemático
para a afirmação que se faz usualmente de que as componentes do campo elétrico paralelas ao
eixo-x, dEP, se anulam. Apenas as componentes normais ao
eixo-x, dEN, contribuem para o campo elétrico total (Figura 6).
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}\left(-0\;\mathbf{i}+2\operatorname{sen}\theta_{m}\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}2\operatorname{sen}\theta_{m}\;\mathbf{j}\\
\mathbf{E}=\frac{\lambda}{2\pi \epsilon_{0}y}\operatorname{sen}\theta_{m}\;\mathbf{j} \tag{XII}
\end{gather}
\]
A densidade linear de carga do fio todo é dada por
\[
\begin{gather}
\lambda=\frac{Q}{L} \tag{XIII}
\end{gather}
\]
substituindo a expressão (XIII) na expressão (XII)
\[
\begin{gather}
\mathbf{E}=\frac{Q}{2\pi \epsilon_{0}yL}\operatorname{sen}\theta_{m}\;\mathbf{j} \tag{XIV}
\end{gather}
\]
O seno de θm pode ser obtido da Figura 7
\[
\begin{gather}
\operatorname{sen}\theta_{m}=\frac{\frac{L}{2}}{r}\\[5pt]
\operatorname{sen}\theta_{m}=\frac{L}{2r} \tag{XV}
\end{gather}
\]
A hipotenusa r é dada pelo Teorema de Pitágoras
\[
\begin{gather}
r^{2}=y^{2}+\left(\frac{L}{2}\right)^{2}\\[5pt]
r^{2}=y^{2}+\frac{L^{2}}{4}\\[5pt]
r=\sqrt{y^{2}+\frac{L^{2}}{4}\;}\\[5pt]
r=\sqrt{\frac{4y^{2}+L^{2}}{4}\;}\\[5pt]
r=\frac{\sqrt{4y^{2}+L^{2}\;}}{2} \tag{XVI}
\end{gather}
\]
substituindo a expressão (XVI) na expressão (XV)
\[
\begin{gather}
\operatorname{sen}\theta_{m}=\frac{L}{\cancel{2}\dfrac{\sqrt{4y^{2}+L^{2}\;}}{\cancel{2}}}\\[5pt]
\operatorname{sen}\theta_{m}=\frac{L}{\sqrt{4y^{2}+L^{2}\;}} \tag{XVII}
\end{gather}
\]
substituindo a expressão (XVII) na expressão (XIV)
\[
\mathbf{E}=\frac{Q}{2\pi \epsilon_{0}y\cancel{L}}\frac{\cancel{L}}{\sqrt{4y^{2}+L^{2}\;}}\;\mathbf{j}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{Q}{2\pi \epsilon_{0}y}\frac{1}{\sqrt{4y^{2}+L^{2}}}\;\mathbf{j}}
\]
publicidade
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .