Solved Problem on Coulomb's Law and Electric Field
Português
English
advertisement
A charge Q is uniformly distributed along a straight wire of length L. Determine the
electric field vector at the points to a distance from the wire along the perpendicular bisector to the
wire.
Problem data:
- Wire length: L;
- Wire charge: Q.
The position vector r goes from an element of charge dq to point P where we want to calculate the electric field, the vector rq locates the charge element relative to the origin of the reference frame, and the vector rp locates point P (Figure 1- A).
\[
\mathbf{r}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\]
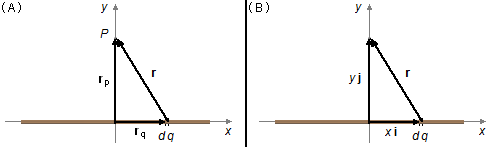
From the geometry of the problem we choose Cartesian coordinates, the rq vector only has a component in the direction i, which is written as \( {\mathbf{r}}_{q}=x\;\mathbf{i} \) and the rp vector only has a component in the j direction, which is written as \( {\mathbf{r}}_{p}=y\;\mathbf{j} \) (Figure 1-B), then the vector position will be
\[
\begin{gather}
\mathbf{r}=y\;\mathbf{j}-x\;\mathbf{i} \tag{I}
\end{gather}
\]
From expression (I), the magnitude of the position vector r will be
\[
\begin{gather}
r^{2}=(-x)^{2}+y^{2}\\
r=\left(x^{2}+y^{2}\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
Solution
The electric field vector is given by
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{III}
\end{gather}
\]
Using the expression of the linear density of charge λ, we have the charge element dq
\[ \bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\]
\[
\begin{gather}
dq=\lambda \;ds \tag{IV}
\end{gather}
\]
where ds is an element of length of the wire
\[
\begin{gather}
ds=dx \tag{V}
\end{gather}
\]
substituting the expression (V) into expression (IV)
\[
\begin{gather}
dq=\lambda \;dx \tag{VI}
\end{gather}
\]
Substituting expressions (I), (II), and (VI) into expression (III)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int {\frac{\lambda\;dx}{\left[\left(x^{2}+y^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda\;dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right) \tag{VII}
\end{gather}
\]
As the charge density λ is constant, it is moved outside of the integral
\[
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int{\frac{dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)
\]
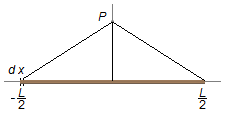
As point P is on the straight line that divides the wire in half, the integral will be made on
all elements of length dx going from
\( -{\frac{L}{2}} \)
to
\( \frac{L}{2} \)
(Figure 2)
\[
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)
\]
factoring y in the numerator and y2 in the denominator
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{\left[y^{2}\left(1+\dfrac{x^{2}}{y^{2}}\right)\right]^{\frac{3}{2}}}}y\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{\left(y^{2}\right)^{\frac{3}{2}}\left[1+\left(\dfrac{x}{y}\right)^{2}\right]^{\frac{3}{2}}}}y\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{\cancelto{2}{3}}\left[1+\left(\dfrac{x}{y}\right)^{2}\;\right]^{\frac{3}{2}}}}\cancel{y}\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\dfrac{x}{y}\right)^{2}\right]^{\frac{3}{2}}}}\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right) \tag{VIII}
\end{gather}
\]
Considering the angle θ measured between the y-axis and the distance r of the
charge element to point P, the tangent of this angle will be (Figure 3)
\[
\begin{gather}
\tan \theta =\frac{x}{y} \\
x=y\tan \theta \tag{IX}
\end{gather}
\]
substituting the expression (IX) into expression (VIII)
\[
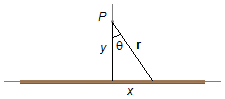
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\dfrac{\cancel{y}\tan \theta}{\cancel{y}}\right)^{2}\right]^{\frac{3}{2}}}}\left(-{\frac{\cancel{y}\tan \theta}{\cancel{y}}}\;\mathbf{i}+\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\tan \theta\right)^{2}\right]^{\frac{3}{2}}}}\left(-\tan \theta\;\mathbf{i}+\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{\mathit{dx}}{y^{2}\left(1+\tan ^{2}\theta\right)^{\frac{3}{2}}}}\left(-\tan \theta\;\mathbf{i}+\;\mathbf{j}\right) \tag{X}
\end{gather}
\]
From the expression (IX), we have the element of length dx relative to the arc element
dθ.
Derivative of
\( x=y\tan \theta \)
\[
\frac{dx}{d\theta}=y\frac{d}{d\theta}\left(\tan \theta \right)
\]
rewriting
\( \tan \theta=\dfrac{\sin \theta}{\cos \theta} \)
we have the derivative of a quotient of functions given by the formula
\[
\left(\frac{u}{v}\right)^{\Large '}=\frac{u'v-u\;v'}{v^{2}}
\]
\[
\begin{align}
\frac{d}{d\theta}\left(\tan \theta \right)=\frac{d}{d\theta}\left(\frac{\sin \theta}{\cos \theta}\right) &=\frac{\cos\theta \cos \theta-\sin \theta (-\sin \theta)}{(\cos \theta)^{2}}=\\ &=\frac{\cos ^{2}\theta+\sin ^{2}\theta}{\cos ^{2}\theta}=\frac{1}{\cos^{2}\theta}
\end{align}
\]
\[
\begin{gather}
\frac{dx}{d\theta}=y\frac{1}{\cos ^{2}\theta}
\end{gather}
\]
Note: The books on Integral and Differential Calculus give the derivative of the
tangent in form
\( \left(\tan \theta \right)^{'}=\sec ^{2}\theta \),
where
\( \sec \theta=\dfrac{1}{\cos \theta} \),
but here for reasons of subsequent simplifications we will let the derivative in the form
shown above.
\[
\begin{gather}
dx=y\frac{1}{\cos ^{2}\theta}\;d\theta \tag{XI}
\end{gather}
\]
substituting the definition of tangent and expression (XI) into expression (X)
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{1}{y^{\cancel{2}}\left[1+\left(\dfrac{\sin \theta}{\cos \theta}\;\right)^{2}\;\right]^{\frac{3}{2}}}}\cancel{y}\;\frac{d\theta}{\cos^{2}\theta}\;\left(\;-\frac{\sin \theta}{\cos \theta}\;\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{1}{y\left[1+\left(\dfrac{\sin \theta}{\cos \theta}\;\right)^{2}\;\right]^{\frac{3}{2}}}}\;\frac{d\theta}{\cos^{2}\theta}\;\left(\;-\frac{\sin \theta}{\cos \theta}\;\mathbf{i}+\;\mathbf{j}\;\right)
\end{gather}
\]
The limits of integration to the variable θ should be from −θm,
the maximum value measured in the clockwise direction, where x is
\( -{\frac{L}{2}} \),
to θm, the maximum value measured in the counterclockwise direction, where
x is
\( {\frac{L}{2}} \)
(Figure 4).
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi\epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\left(1+\dfrac{\sin ^{2}\theta}{\cos^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\sin \theta}{\cos\theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\left(\dfrac{\cos ^{2}+\sin ^{2}\theta}{\cos ^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos^{2}\theta}\;\left(-{\frac{\sin \theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\left(\dfrac{1}{\cos ^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\sin \theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\dfrac{1}{\left(\cos ^{2}\theta\right)^{\frac{3}{2}}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\sin \theta}{\cos \theta}\;}\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\dfrac{1}{\cos ^{\cancel{3}}\theta}}}\;\frac{d\theta}{\cancel{\cos^{2}\theta}}\left(-{\frac{\sin \theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{1}{y\dfrac{1}{\cos \theta}}}\;d\theta\left(-{\frac{\sin \theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\theta_{m}}}^{{\theta_{m}}}{\frac{\cos\theta}{y}}\;d\theta \left(-{\frac{\sin \theta}{\cos\theta}}\;\mathbf{i}+\;\mathbf{j}\right)
\end{gather}
\]
As y is constant, it is moved outside of the integral and the integral of the sum is equal to the
sum of the integral
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0} y}\left(-\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta\frac{\sin \theta}{\cos \theta}\;d\theta\;\mathbf{i}+\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos\theta \;d\theta\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}\left(\underbrace{-{\int_{{-\theta_{m}}}^{{\theta_{m}}}\sin \theta \;d\theta\;\mathbf{i}}}_{0}+\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta\;\mathbf{j}\right)
\end{gather}
\]
Integration of \( \displaystyle \int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta \)
1st method
As the cosine function is an even function, f(x) = f(−x), we can integrate half of the interval, from 0 to θm, and multiply the integral by 2
We can integrate all the interval, from −θm to θm
1st method
As the cosine function is an even function, f(x) = f(−x), we can integrate half of the interval, from 0 to θm, and multiply the integral by 2
\[
\begin{align}
2\int_{0}^{{\theta_{m}}}\cos \theta \;d\theta &=2\left.\sin \theta \right|_{\;0}^{\;\theta_{m}}=2(\sin \theta_{m}-\sin 0)=\\
&=2(\sin \theta_{m}-0)=2\sin \theta_{m}
\end{align}
\]
2nd method
We can integrate all the interval, from −θm to θm
\[
\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta=\left.\sin \theta \;\right|_{\;-\theta_{m}}^{\;\theta_{m}}=\sin \theta_{m}-\sin (-\theta_{m})
\]
as sine is an odd function, f(−x) = −f(x), we have
\( \sin (-\theta_{m})=-\sin (\theta_{m}) \)
\[
\begin{align}
\int_{{-\theta_{m}}}^{{\theta_{m}}}\cos \theta \;d\theta &=\sin \theta_{m}-(-\sin \theta_{m})=\\
&=\sin \theta_{m}+\sin (\theta_{m})=2\sin \theta_{m}
\end{align}
\]
Integration of \( \displaystyle \int_{{-\theta_{m}}}^{{\theta_{m}}}\sin \theta \;d\theta \)
1st method
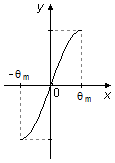
Figure 5
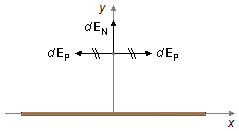Figure 6
1st method
\[
\int_{{-\theta_{m}}}^{{\theta_{m}}}\sin \theta \;d\theta=-\left.\cos \theta \;\right|_{\;-\theta_{m}}^{\;\theta_{m}}=-\left[\cos \theta_{m}-\cos (-\theta_{m})\right]
\]
as cosine is an odd function, f(x) = f(−x), we have
\( \cos (\theta_{m})=\cos (-\theta_{m}) \)
\[
\int_{{-\theta_{m}}}^{{\theta_{m}}}\sin \theta\;d\theta =-(\cos \theta_{m}-\cos \theta_{m})=0
\]
2nd method
The graph of sine between −θm and 0 has a "negative" area below the x-axis, and between 0 and θm a "positive" area above the x-axis, these two areas cancel in the integration, and the integral is equal to zero. in the i direction (Figure 5).
The graph of sine between −θm and 0 has a "negative" area below the x-axis, and between 0 and θm a "positive" area above the x-axis, these two areas cancel in the integration, and the integral is equal to zero. in the i direction (Figure 5).
Figure 5
Note: The integral in the direction i, which is zero, represents the mathematical
calculation for the assertion that is usually done that the components of the electric field parallel
to the x-axis, dEP, cancel. Only the normal components to the
x-axis, dEN, contribute to the total electric field (Figure 6).
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}\left(-0\;\mathbf{i}+2\sin \theta_{m}\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}2\sin \theta_{m}\;\mathbf{j}\\
\mathbf{E}=\frac{\lambda}{2\pi \epsilon_{0}y}\sin \theta_{m}\;\mathbf{j} \tag{XII}
\end{gather}
\]
The linear density of charges can be written
\[
\begin{gather}
\lambda=\frac{Q}{L} \tag{XIII}
\end{gather}
\]
substituting the expression (XIII) into expression (XII)
\[
\begin{gather}
\mathbf{E}=\frac{Q}{2\pi \epsilon_{0}yL}\sin \theta_{m}\;\mathbf{j} \tag{XIV}
\end{gather}
\]
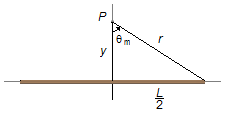
The sine of θm can be obtained from Figure 7
\[
\begin{gather}
\sin \theta_{m}=\frac{\frac{L}{2}}{r}\\[5pt]
\sin \theta_{m}=\frac{L}{2r} \tag{XV}
\end{gather}
\]
The hypotenuse r is given by the Pythagorean Theorem
\[
\begin{gather}
r^{2}=y^{2}+\left(\frac{L}{2}\right)^{2}\\[5pt]
r^{2}=y^{2}+\frac{L^{2}}{4}\\[5pt]
r=\sqrt{y^{2}+\frac{L^{2}}{4}\;}\\[5pt]
r=\sqrt{\frac{4y^{2}+L^{2}}{4}\;}\\[5pt]
r=\frac{\sqrt{4y^{2}+L^{2}\;}}{2} \tag{XVI}
\end{gather}
\]
substituting the expression (XVI) into expression (XV)
\[
\begin{gather}
\sin \theta_{m}=\frac{L}{\cancel{2}\dfrac{\sqrt{4y^{2}+L^{2}\;}}{\cancel{2}}}\\[5pt]
\sin \theta_{m}=\frac{L}{\sqrt{4y^{2}+L^{2}\;}} \tag{XVII}
\end{gather}
\]
substituting the expression (XVII) into expression (XIV)
\[
\mathbf{E}=\frac{Q}{2\pi \epsilon_{0}y\cancel{L}}\frac{\cancel{L}}{\sqrt{4y^{2}+L^{2}\;}}\;\mathbf{j}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{Q}{2\pi \epsilon_{0}y}\frac{1}{\sqrt{4y^{2}+L^{2}}}\;\mathbf{j}}
\]
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .