Exercício Resolvido de Movimento Unidimensional

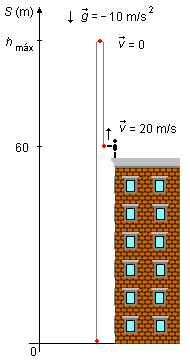
Do alto de um prédio de 60 m uma pedra é lançada verticalmente para cima com velocidade inicial de 20 m/s. Determinar:
a) O tempo de subida da pedra;
b) A altura máxima em relação ao solo;
c) Depois de quanto tempo após o lançamento a pedra atinge o solo;
d) A velocidade da pedra ao atingir o solo;
e) Construir os gráficos do espaço em função do tempo e da velocidade em função do tempo.
Dada aceleração da gravidade igual a 10 m/s².

Dados do problema:

Altura de lançamento da pedra: S₀ = 60 m;
Velocidade inicial da pedra: v₀ = 20 m/s;
Aceleração da gravidade: g = 10 m/s².

Esquema do problema:

Adotando-se um sistema de referência orientado para cima, h_máx é a altura máxima atingida pela pedra, a velocidade inicial terá sinal positivo, está no mesmo sentido do eixo de referência, a aceleração da gravidade terá sinal negativo, está no sentido contrário à orientação do eixo de referência.

Figura 1

Solução:

a) A função horária da velocidade é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0-gt} \end{gather} \]

substituindo os dados do problema na equação para a velocidade

\[ \begin{gather} v=20-10t \tag{I} \end{gather} \]

a pedra vai subir até a velocidade se anular, v = 0

\[ \begin{gather} 0=20-10t\\ 10t=20\\ t=\frac{20}{10} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {t=2\;\mathrm s} \end{gather} \]

b) A função horária do espaço percorrido é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t-\frac{g}{2}t^2} \end{gather} \]

substituindo os dados temos na equação horária do movimento

\[ \begin{gather} S=60+20t-\frac{10}{2}t^2\\ S=60+20t-5t^2 \tag{II} \end{gather} \]

substituindo o tempo encontrado no item anterior e fazendo S = h_max

\[ \begin{gather} h_{max}=60+20.2-5.2^2\\ h_{max}=60+40-5.4 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {h_{max}=80\;\mathrm m} \end{gather} \]

c) Quando a pedra atinge o solo temos S = 0, substituindo este valor na equação (II)

\[ \begin{gather} -5t^2+20t+60=0 \end{gather} \]

dividindo ambos os lados da equação por −5

\[ \begin{gather} t^2-4t-12=0 \end{gather} \]

Esta é uma Equação do 2.º Grau onde a incógnita é o valor desejado t

Solução da Equação de 2.º Grau \( t^2-4 t-12=0 \)

\[ \begin{array}{l} \Delta=b^2-4ac=(-4)^2-4\times 1\times (-12)=16+48=64 \\[10pt] t=\dfrac{-b\pm \sqrt{\Delta}}{2a}=\dfrac{-(-4)\pm \sqrt{64}}{2\times 1}=\dfrac{4\pm 8}{2} \end{array} \]

as duas raízes da equação são

\[ \begin{gather} t_{1}=6\;\mathrm s \qquad\text{e}\qquad t_{2}=-2\;\mathrm s \end{gather} \]

desprezando a segunda raiz, não existe tempo negativo, o tempo que leva para a pedra atingir o solo é de 6 s.

d) Substituindo o valor para o tempo encontrado no item anterior na equação (I) da velocidade

\[ \begin{gather} v=20-10\times 6 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {v=-40\;\mathrm{m/s}} \end{gather} \]

o sinal de negativo indica que a velocidade final está apontada para baixo, contra o sentido do eixo de referência.

e) Gráfico do espaço percorrido em função do tempo, S = f(t).
Usando a equação (II) atribuímos valores a t e obtemos S, construindo a Tabela 1 e com os valores da tabela fazemos o Gráfico 1

t (s)	`\( S(t)=60+20t-5t^2 \)`	S(t) (m)
0	`\( S(0)=60+20\times 0-5\times 0^2 \)`	60
2	`\( S(2)=60+20\times 2-5\times 2^2 \)`	80
4	`\( S(4)=60+20\times 4-5\times 4^2 \)`	60
6	`\( S(6)=60+20\times 6-5\times 6^2 \)`	0

Tabela 1

Gráfico 1

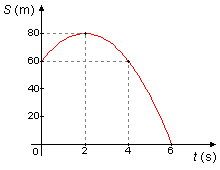
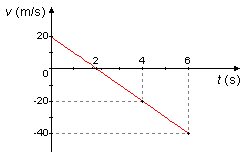
Gráfico da velocidade em função do tempo, v = f(t).
Usando a equação (I) atribuímos valores a t e obtemos v, construindo a Tabela 2 e com os valores da tabela fazemos o Gráfico 2

t (s)	`\( v(t)=20t-10t \)`	v(t) (m/s)
0	`\( v(0)=20\times 0-10\times 0 \)`	20
2	`\( v(2)=20\times 2-10\times 2 \)`	0
4	`\( v(4)=20\times 4-10\times 4 \)`	−20
6	`\( v(6)=20\times 6-10\times 6 \)`	−40

Tabela 2

Gráfico 2