Solved Problem on One-dimensional Motion

From the top of a building with 60 m, a stone is thrown vertically upwards with an initial speed of 20 m/s. Determine:
a) The time interval of the rise of the stone;
b) The maximum height above the ground;
c) After how long after launching the stone hits the ground;
d) The speed of the stone hits the ground;
e) Construct a graph of displacement versus time and velocity versus time.
Assume the acceleration due to gravity is equal to 10 m/s².

Problem data:

Height of stone release: S₀ = 60 m;
Initial speed of stone: v₀ = 20 m/s;
Acceleration due to gravity: g = 10 m/s².

Problem diagram:

We choose a reference frame pointing upwards, h_max is the maximum height reached by the stone, the initial speed has a positive sign, is in the same direction of the reference frame, the acceleration due to gravity has a negative sign, it is in the opposite direction of the reference frame.

Figure 1

Solution

a) The equation velocity as a function of time is given by

\[ \bbox[#99CCFF,10px] {v=v_{0}-gt} \]

substituting the data given in the problem in the equation for the velocity

\[ \begin{gather} v=20-10t \tag{I} \end{gather} \]

the stone will rise until the speed becomes zero, v = 0

\[ \begin{gather} 0=20-10t\\ 10t=20\\ t=\frac{20}{10} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {t=2\;\text{s}} \]

b) The equation of displacement as a function of time with acceleration due to gravity is given by

\[ \bbox[#99CCFF,10px] {S=S_{0}+v_{0}t-\frac{g}{2}t^{2}} \]

substituting the data, we have the expression

\[ \begin{gather} S=60+20t-\frac{10}{2}t^{2}\\ S=60+20t-5t^{2} \tag{II} \end{gather} \]

substituting the time found in the previous item and setting S = h_max

\[ \begin{gather} h_{max}=60+20\times 2-5\times 2^{2}\\ h_{max}=60+40-5\times 4 \end{gather} \]

\[ \bbox[#FFCCCC,10px] {h_{max}=80\;\text{m}} \]

c) When the stone hits the ground, we have S = 0, substituting this value into the expression (II)

\[ -5t^{2}+20t+60=0 \]

dividing both sides of the equation by −5

\[ t^{2}-4t-12=0 \]

This is a Quadratic Equation, where the unknown is the value t

Solution of the Quadratic Equation \( t^{2}-4 t-12=0 \)

\[ \begin{array}{l} \Delta=b^{2}-4ac=(-4)^{2}-4\times 1\times (-12)=16+48=64\\[10pt] t=\dfrac{-b\pm \sqrt{\Delta}}{2a}=\dfrac{-(-4)\pm \sqrt{64}}{2\times 1}=\dfrac{4\pm 8}{2} \end{array} \]

the two roots of the equation are

\[ \begin{gather} t_{1}=6\;\text{s}\\ \qquad\text{e}\qquad\\ t_{2}=-2\;\text{s} \end{gather} \]

neglecting the second root, there is no negative time, the time interval it takes for the stone hits the ground is 6 s.

d) Substituting the value for the time found in the previous item into the expression (I)

\[ v=20-10\times 6 \]

\[ \bbox[#FFCCCC,10px] {v=-40\;\text{m/s}} \]

the negative sign indicates that the final velocity is pointed downward, in the opposite direction of the reference frame.

e) Graph of displacement versus time, S = f(t).
Using the expression (II) assign values to t to obtain S, we have Table 1 and construct Graph 1

t (s)	`\( S(t)=60+20t-5t^{2} \)`	S(t) (m)
0	`\( S(0)=60+20\times 0-5\times 0^{2} \)`	60
2	`\( S(2)=60+20\times 2-5\times 2^{2} \)`	80
4	`\( S(4)=60+20\times 4-5\times 4^{2} \)`	60
6	`\( S(6)=60+20\times 6-5\times 6^{2} \)`	0

Table 1

Graph 1

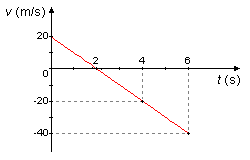
Graph of velocity versus time, v = f(t).
Using the expression (I) assign values to t to obtain v, we have Table 2 and construct Graph 2

t (s)	`\( v(t)=20t-10t \)`	v(t) (m/s)
0	`\( v(0)=20\times 0-10\times 0 \)`	20
2	`\( v(2)=20\times 2-10\times 2 \)`	0
4	`\( v(4)=20\times 4-10\times 4 \)`	−20
6	`\( v(6)=20\times 6-10\times 6 \)`	−40

Table 2

Graph 2

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .