Exercício Resolvido de Movimento Unidimensional
publicidade
Calcule a relação entre as alturas atingidas por dois corpos lançados verticalmente para cima, com velocidades iniciais iguais, um na Terra, outro na Lua. Sabe-se que a aceleração da gravidade na Terra é 6 vezes maior do que na Lua.
Dados do problema:
- Relação entre a aceleração da gravidade na Terra e na Lua: \( g_{\small T}=6\;g_{\small L} \).
Adotamos um sistema de referência orientado para cima com origem no ponto de lançameto, nos dois casos, como as acelerações da gravidade apontam para o solo, seus sinais são negativos. As velocidades iniciais apontam para cima, seus sinais são positivos (Figura 1).
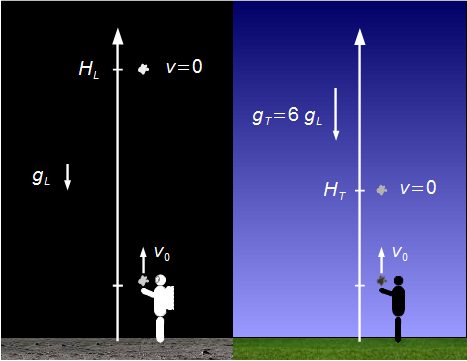
Solução
Para encontrar a altura máxima que corpo atinge, usamos a Equação de Torricceli, escrevendo para os dois corpos
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v^{2}=v_{0}^{2}+2a\Delta S}
\end{gather}
\]
- Para a Lua
\[
\begin{gather}
v^{2}=v_{0}^{2}+2g_{\small L}\Delta S_{\small L}\\[5pt]
v^{2}=0^{2}+2g_{\small L}H_{\small L}\\[5pt]
v^{2}=2g_{\small L}H_{\small L}\\[5pt]
H_{\small L}=\frac{v^{2}}{2g_{\small L}} \tag{I}
\end{gather}
\]
- Para a Terra
\[
\begin{gather}
v^{2}=v_{0}^{2}+2g_{\small T}\Delta S_{\small T}\\[5pt]
v^{2}=0^{2}+2g_{\small T}H_{\small T}\\[5pt]
v^{2}=2g_{\small T}H_{\small T}\\[5pt]
H_{\small T}=\frac{v^{2}}{2g_{\small T}} \tag{II}
\end{gather}
\]
dividindo a equação (I) pela equação (II)
\[
\begin{gather}
\frac{H_{\small L}}{H_{\small T}}=\frac{\dfrac{v^{2}}{2g_{\small L}}}{\dfrac{v^{2}}{2g_{\small T}}}\\[5pt]
\frac{H_{\small L}}{H_{\small T}}=\frac{v^{2}}{2g_{\small L}}\frac{2g_{\small T}}{v^{2}}\\[5pt]
\frac{H_{\small L}}{H_{\small T}}=\frac{g_{\small T}}{g_{\small L}}
\end{gather}
\]
substituindo a razão entre as acelerações da gravidade na Terra e na Lua dadas no problema
\[
\begin{gather}
\frac{H_{\small L}}{H_{\small T}}=\frac{6\cancel{g_{\small L}}}{\cancel{g_{\small L}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{H_{\small L}=6\;H_{\small T}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .