Solved Problem on One-dimensional Motion

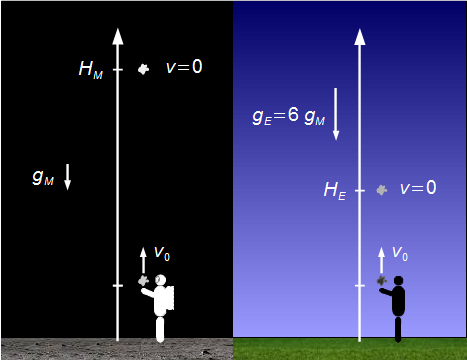
Calculate the relationship between the heights reached by two bodies launched vertically upwards, with equal initial speeds, one on Earth, the other on the Moon. It is known that the acceleration due to gravity on Earth is 6 times greater than on the Moon.

Problem data:

Relationship between the acceleration of gravity on the Earth and the Moon: \( g_{\small E}=6\;g_{\small M} \).

Problem diagram:

We choose a reference frame pointing upwards with origin at the launch point. In both cases, as the accelerations due to gravity point towards the ground, their signs are negative. The initial velocities point upwards, their signs are positive (Figure 1).

Figure 1

Solution

To find the maximum height that the body reaches, we use the equation of velocity as a function of displacement, writing for both bodies

\[ \begin{gather} \bbox[#99CCFF,10px] {v^{2}=v_{0}^{2}+2a\Delta S} \end{gather} \]

For the Moon

\[ \begin{gather} v^{2}=v_{0}^{2}+2g_{\small M}\Delta S_{\small M}\\[5pt] v^{2}=0^{2}+2g_{\small M}H_{\small M}\\[5pt] v^{2}=2g_{\small M}H_{\small M}\\[5pt] H_{\small M}=\frac{v^{2}}{2g_{\small M}} \tag{I} \end{gather} \]

For the Earth

\[ \begin{gather} v^{2}=v_{0}^{2}+2g_{\small E}\Delta S_{\small E}\\[5pt] v^{2}=0^{2}+2g_{\small E}H_{\small E}\\[5pt] v^{2}=2g_{\small E}H_{\small E}\\[5pt] H_{\small E}=\frac{v^{2}}{2g_{\small E}} \tag{II} \end{gather} \]

dividing equation (I) by equation (II)

\[ \begin{gather} \frac{H_{\small M}}{H_{\small E}}=\frac{\dfrac{v^{2}}{2g_{\small M}}}{\dfrac{v^{2}}{2g_{\small E}}}\\[5pt] \frac{H_{\small M}}{H_{\small E}}=\frac{v^{2}}{2g_{\small M}}\frac{2g_{\small E}}{v^{2}}\\[5pt] \frac{H_{\small M}}{H_{\small E}}=\frac{g_{\small E}}{g_{\small M}} \end{gather} \]

substituting the ratio between the accelerations due to gravity on the Earth and on the Moon given in the problem

\[ \begin{gather} \frac{H_{\small M}}{H_{\small E}}=\frac{6\cancel{g_{\small M}}}{\cancel{g_{\small M}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {H_{\small M}=6\;H_{\small E}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .