Exercício Resolvido de Movimento Unidimensional
publicidade
De uma plataforma situada a uma altura h acima do solo é abandonado um objeto, no mesmo instante outro é lançado do solo segundo a mesma vertical ascendente com velocidade inicial v0. Sabendo-se que os dois objetos se encontram na metade da altura, calcular h em função de v0 e da aceleração da gravidade g.
Dados do problema:
- Altura da plataforma: h;
- Velocidade inicial do objeto abandonado do alto: v01 = 0;
- Velocidade inicial do objeto lançado para cima: v02 = v0;
- Aceleração da gravidade: g.
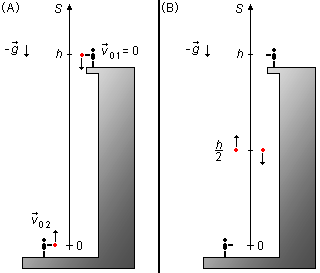
Adotamos um sistema de referência orientado de baixo para cima com origem na parte mais baixa de onde é lançado o objeto para cima. A aceleração da gravidade está orientada no sentido contrário da trajetória e é negativa, g < 0. Para o objeto que é abandonado do alto da plataforma sua posição inicial será S01 = h. O objeto lançado de baixo está na origem, sua posição inicial será S0 = 0 (Figura 1-A).
Solução
A expressão para os movimentos de queda livre e lançamento vertical é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_{0}+v_{0}t-\frac{g}{2}t^{2}} \tag{I}
\end{gather}
\]
Aplicando a expressão (I) para o objeto em queda livre
\[
\begin{gather}
S_{1}=S_{01}+v_{01}t-\frac{g}{2}t^{2}\\[5pt]
S_{1}=h+0.t-\frac{g}{2}t^{2}\\[5pt]
S_{1}=h-\frac{g}{2}t^{2} \tag{II}
\end{gather}
\]
Aplicando a expressão (I) para o objeto lançado verticalmente
\[
\begin{gather}
S_{2}=S_{02}+v_{02}t-\frac{g}{2}t^{2}\\[5pt]
S_{2}=0+v_{0}t-\frac{g}{2}t^{2}\\[5pt]
S_{2}=v_{0}t-\frac{g}{2}t^{2} \tag{III}
\end{gather}
\]
Quando os objetos se encontram temos a condição de que estão na metade da queda, substituindo a condição,
\( S_{1}=\dfrac{h}{2} \),
na expressão (II)
\[
\begin{gather}
\frac{h}{2}=h-\frac{g}{2}t^{2}\\[5pt]
\frac{g}{2}t^{2}=h-\frac{h}{2}
\end{gather}
\]
do lado direito da igualdade multiplicamos e dividimos o primeiro termo por 2
\[
\begin{gather}
\frac{g}{2}t^{2}=h.\frac{2}{2}-\frac{h}{2}\\[5pt]
\frac{g}{2}t^{2}=\frac{2h-h}{2}\\[5pt]
\frac{g}{\cancel{2}}t^{2}=\frac{h}{\cancel{2}}\\[5pt]
gt^{2}=h\\[5pt]
t=\sqrt{\frac{h}{g}} \tag{IV}
\end{gather}
\]
Como os objetos se encontram na metade da altura
\( S_{2}=\dfrac{h}{2} \),
substituindo este valor e o valor encontrado em (IV) na expressão (III)
\[
\begin{gather}
\frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}-\frac{g}{2}\left(\sqrt{\frac{h}{g}}\right)^{2}\\[5pt]
\frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}-\frac{\cancel{g}}{2}\frac{h}{\cancel{g}}\\[5pt]
\frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}-\frac{h}{2}\\[5pt]
\frac{h}{2}+\frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}\\[5pt]
h=v_{0}\sqrt{\frac{h}{g}}
\end{gather}
\]
elevando os dois lados da igualdade ao quadrado
\[
\begin{gather}
h^{2}=\left(v_{0}\sqrt{\frac{h}{g}}\right)^{2}\\[5pt]
h^{2}=v_{0}^{2}\frac{h}{g}\\[5pt]
\frac{h^{\cancel{2}}}{\cancel{h}}=\frac{v_{0}^{2}}{g}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{h=\frac{v_{0}^{2}}{g}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .