Solved Problem on One-dimensional Motion
advertisement   



From a platform at a height h above the ground, an object is released, at the same instant, another object is launched from the ground to the same upward direction with initial speed v0. The two objects meet in half of the height, calculate h as a function of v0 and the acceleration due to gravity g.


Problem data:
  • Platform height:    h;
  • Initial speed of the released object of the top:    v01 = 0;
  • Initial speed of the object launched from the ground:    v02 = v0;
  • Acceleration due to gravity:    g.
Problem diagram:

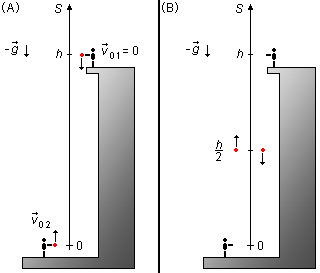
We choose a reference frame pointing in the upwards direction with origin on the ground where the object is released. The acceleration due to gravity is in the opposite direction of the reference frame and is negative, g < 0. For the object released from the top of the platform, its initial position will be S01 = h. The object released from the ground is at the origin, its initial position will be S0 = 0 (Figure 1-A).

Figure 1

Solution

The expression for free fall and vertical launch is given by
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_{0}+v_{0}t-\frac{g}{2}t^{2}} \tag{I} \end{gather} \]
Applying the expression (I) to the object in free fall
\[ \begin{gather} S_{1}=S_{01}+v_{01}t-\frac{g}{2}t^{2}\\[5pt] S_{1}=h+0.t-\frac{g}{2}t^{2}\\[5pt] S_{1}=h-\frac{g}{2}t^{2} \tag{II} \end{gather} \]
Applying the expression (i) to the object launched from the ground
\[ \begin{gather} S_{2}=S_{02}+v_{02}t-\frac{g}{2}t^{2}\\[5pt] S_{2}=0+v_{0}t-\frac{g}{2}t^{2}\\[5pt] S_{2}=v_{0}t-\frac{g}{2}t^{2} \tag{III} \end{gather} \]
When objects meet, we have the condition that they are in the middle of the fall, substituting the condition \( S_{1}=\dfrac{h}{2} \), into the expression (II)
\[ \begin{gather} \frac{h}{2}=h-\frac{g}{2}t^{2}\\[5pt] \frac{g}{2}t^{2}=h-\frac{h}{2} \end{gather} \]
on the right-hand side of the equation we multiply and divide the first term by 2
\[ \begin{gather} \frac{g}{2}t^{2}=h.\frac{2}{2}-\frac{h}{2}\\[5pt] \frac{g}{2}t^{2}=\frac{2h-h}{2}\\[5pt] \frac{g}{\cancel{2}}t^{2}=\frac{h}{\cancel{2}}\\[5pt] gt^{2}=h\\[5pt] t=\sqrt{\frac{h}{g}} \tag{IV} \end{gather} \]
As objects meeting in halfway, we also have \( S_{2}=\dfrac{h}{2} \), substituting this value and the value found in (IV) into the expression (III)
\[ \begin{gather} \frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}-\frac{g}{2}\left(\sqrt{\frac{h}{g}}\right)^{2}\\[5pt] \frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}-\frac{\cancel{g}}{2}\frac{h}{\cancel{g}}\\[5pt] \frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}-\frac{h}{2}\\[5pt] \frac{h}{2}+\frac{h}{2}=v_{0}\sqrt{\frac{h}{g}}\\[5pt] h=v_{0}\sqrt{\frac{h}{g}} \end{gather} \]
squaring the two sides of the equation
\[ \begin{gather} h^{2}=\left(v_{0}\sqrt{\frac{h}{g}}\right)^{2}\\[5pt] h^{2}=v_{0}^{2}\frac{h}{g}\\[5pt] \frac{h^{\cancel{2}}}{\cancel{h}}=\frac{v_{0}^{2}}{g} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {h=\frac{v_{0}^{2}}{g}} \end{gather} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .